Магнитное состояние машины, определяющее синхронное индуктивное сопротивление по продольной оси. Уравнения напряжений синхронной машины. Модель машины с вращающимися щетками при неподвижной обмотке статора, страница 2

.                (1.21)

Физическое истолкование поперечной индуктивности  может быть дано аналогично . Отличие создаваемого синхронного режима машины заключается лишь в том, что амплитуда магнитного поля должна совпадать с поперечной осью полюсов q. В этом случае  и соотношения потокосцепления  и тока фазной обмотки  определяет индуктивность по поперечной оси машины

.

Таким образом, представляет индуктивность фазной обмотки статора при протекании по обмоткам статора симметричных синусоидальных токов прямой последовательности, вращении ротора с синхронной частотой и ориентации поля токов статора по поперечной оси машины. Соответствующее сопротивление  называется синхронным индуктивным сопротивлением по поперечной оси. На рис. 1.9 показаны состояние обмоток машины (а) и пути магнитных потоков (б), определяющие сопротивление обмотки статора, равное .

Если в режиме ориентации магнитного поля по оси q (рис. 1.9) выполнить замеры фазного напряжения  тока  синхронной машины, то можно для данной оси определить индуктивное сопротивление

.                                (1.22)

Однако при таком методе определения  и  возникают значительные трудности, связанные с совмещением определенных осей ротора с амплитудой магнитного поля. Поэтому на практике используются более простые методы определения сопротивлений  и .

В явнополюсной синхронной машине с несимметричным в магнитном отношении ротором  и , что является ее характерной особенностью, существенно отличающей ее от неявнополюсной с практически симметричным магнитопроводом ротора, для которой обычно принимается

                                                                                      (1.23)

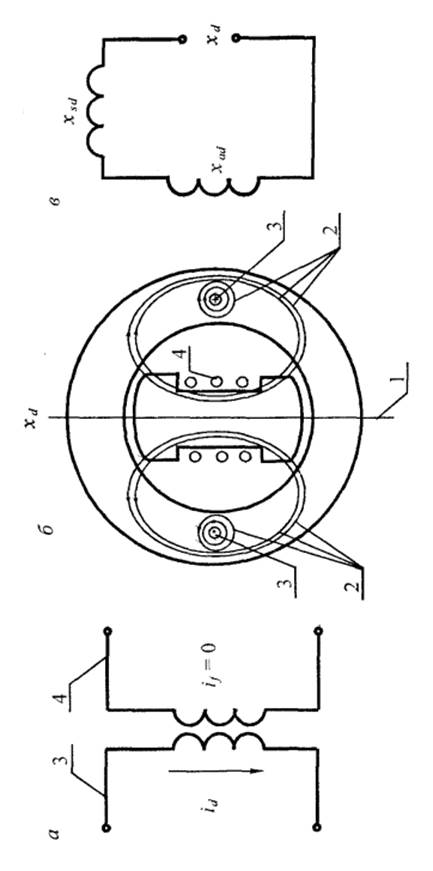
Рис. 1.8. Магнитное состояние машины, определяющее синхронное индуктивное сопротивление по продольной оси: 1 – продольная ось; 2 – магнитный поток; 3 – обмотка статора; 4 – обмотка ротора;                                            а – состояние обмоток; б – пути магнитных потоков; в – схема замещения  .

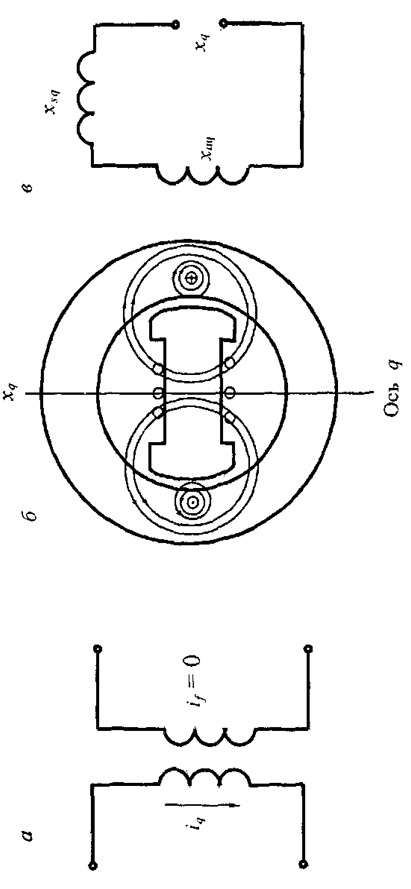
Рис. 1.9. Магнитное состояние машины, когда обмотка статора обладает сопротивлением         (обозначения рис. 1.8).

 – синхронное реактивное сопротивление неявнополюсной машины, определяющее ее поведение при любой симметричной нагрузке токами прямой последовательности.

Анализ рис. 1.8, в показывает, что синхронное индуктивное сопротивление  можно представить в виде суммы двух составляющих - одной, которая соответствует магнитному полю рассеивания обмотки статора , и другой, соответствующей магнитному полю, проходящему через зазор машины по оси d (поле реакции якоря) .

Аналогично, как видно из рис. 1.9, в, синхронное индуктивное сопротивление  можно представить в виде суммы двух составляющих  и  .

Поскольку практически для всех машин , то

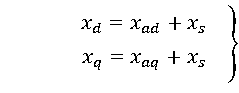                           ,                            (1.24)

где  –  индуктивное сопротивление рассеяния обмотки статора;

,  – индуктивные сопротивления взаимоиндукции между обмотками статора и ротора соответственно по продольной и поперечной осям.

Полученные уравнения позволяют представить сопротивления  и   схемами замещения.  Поскольку уравнения (1.19) потокосцеплений записаны с соблюдением принципа взаимности в отношении индуктивностей магнитосвязанных цепей ротора и статора, то очевидно, что .

Это означает равенство индуктивных сопротивлений взаимоиндукции обмоток как со стороны статора, так и со стороны ротора. По аналогии собственное сопротивление ротора равно:

,                 (1.25)

где – индуктивное сопротивление рассеяния обмотки возбуждения.

Для принимаемых обычно базисных величин сопротивлений () и индуктивностей ), связанных соотношением , относительные значения индуктивностей и соответствующих им индуктивных сопротивлений равны друг другу (например,                                                .

Поэтому уравнения потокосцеплений (1.19) в относительных единицах можно записать в виде:

                                                    (1.26)

1.1.2.2. Уравнения напряжений синхронной машины

Формальная связь между действительными фазными напряжениями синхронной машины и напряжениями в осях  d и q дана в уравнении (1.17).