Необходимо
получить выражения продольной ![]() и поперечной
и поперечной ![]() составляющих напряжений
через параметры машины в рассматриваемых осях d, q. Для этого подставим в уравнение
(1.17) выражения (1.3) для фазных напряжений и после преобразований с учетом
(1.12) и (1.16) получим
составляющих напряжений
через параметры машины в рассматриваемых осях d, q. Для этого подставим в уравнение
(1.17) выражения (1.3) для фазных напряжений и после преобразований с учетом
(1.12) и (1.16) получим
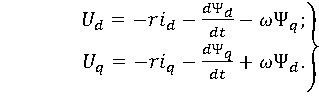 . (1.27)
. (1.27)
Данные уравнения напряжений синхронной машины в осях d и q были получены независимо друг от друга американским инженером Р. Парком и советским ученым А. А. Горевым, поэтому в литературе они обычно называются уравнениями Парка – Горева.
Дадим
физическую интерпретацию отдельным составляющим полученных уравнений.
Произведение активного сопротивления фазной обмотки на токи (![]() ) и (
) и (![]() ) являются
омическими падениями напряжения в продольной и поперечной обмотке статора. Две
другие составляющие в уравнениях являются функциями потокосцеплений. В переходном
процессе потокосцепления
) являются
омическими падениями напряжения в продольной и поперечной обмотке статора. Две
другие составляющие в уравнениях являются функциями потокосцеплений. В переходном
процессе потокосцепления ![]() и
и ![]() изменяются по абсолютной
величине (пульсируют). Изменения потокосцеплений приводят к появлению в
обмотке по оси d ЭДС
изменяются по абсолютной
величине (пульсируют). Изменения потокосцеплений приводят к появлению в
обмотке по оси d ЭДС ![]() , а в обмотке по оси q ЭДС
, а в обмотке по оси q ЭДС ![]() . В
литературе часто составляющие
. В
литературе часто составляющие ![]() и
и ![]() и
называет трансформаторными ЭДС. Это связано с тем, что при схематичном
изображении обмоток по осям, синхронная машина, например, по оси d, представляет
собой двухобмоточный трансформатор, так как имеет два электромагнитосвязанных
контура (см. рис. 1.7).
и
называет трансформаторными ЭДС. Это связано с тем, что при схематичном
изображении обмоток по осям, синхронная машина, например, по оси d, представляет
собой двухобмоточный трансформатор, так как имеет два электромагнитосвязанных
контура (см. рис. 1.7).
Чтобы понять смысл третьей составляющей в уравнениях (1.27), необходимо по-иному схематично представить синхронную машину.
До
сих пор мы представляли, что ![]() – токи и напряжения в
фиктивных вращающихся обмотках статора (рис. 1.7). Однако не обязательно
предполагать, что фиктивные обмотки по осям d и q вращаются.
Аналогичный результат можно получить, полагая, что обмотки статора неподвижны
(как это и есть в действительности) и присоединены к неподвижному коллектору с
контактными кольцами, по которому скользят щетки, вращающиеся вместе с
ротором. При этом щетки коллектора расположены в продольной и поперечной осях.
В таком случае
– токи и напряжения в
фиктивных вращающихся обмотках статора (рис. 1.7). Однако не обязательно
предполагать, что фиктивные обмотки по осям d и q вращаются.
Аналогичный результат можно получить, полагая, что обмотки статора неподвижны
(как это и есть в действительности) и присоединены к неподвижному коллектору с
контактными кольцами, по которому скользят щетки, вращающиеся вместе с
ротором. При этом щетки коллектора расположены в продольной и поперечной осях.
В таком случае ![]() можно представить как
напряжение на паре щеток, а величину
можно представить как
напряжение на паре щеток, а величину ![]() – как ток статора, протекающий
через эту же пару щеток, ось которой все время совпадает с продольной осью
ротора (рис. 1.10). Аналогичным образом
– как ток статора, протекающий
через эту же пару щеток, ось которой все время совпадает с продольной осью
ротора (рис. 1.10). Аналогичным образом ![]() можно представить как
напряжение на второй паре щеток, а величину
можно представить как
напряжение на второй паре щеток, а величину ![]() – как ток статора,
протекающий через вторую пару щеток, ось которой совпадает с поперечной осью
ротора.
– как ток статора,
протекающий через вторую пару щеток, ось которой совпадает с поперечной осью
ротора.
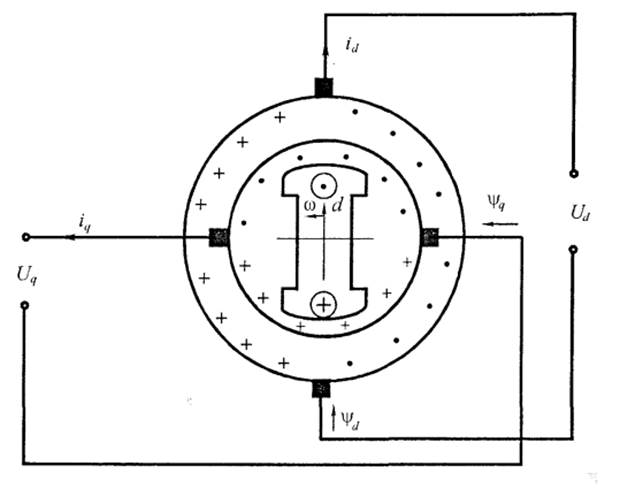
Рис. 1.10. Модель машины с вращающимися щетками при неподвижной обмотке статора
При
таком физическом представлении модели синхронной машины магнитное поле в ней, а
следовательно, и потокосцепление вращаются относительно неподвижных обмоток
статора. При перемещении потокосцеплений ![]() и
и ![]() относительно
обмоток статора, в каждой из них наводится ЭДС вращения. Величина ЭДС вращения
пропорциональна произведению скорости перемещения на составляющую
потокосцепления, направленную вдоль плоскости данной обмотки. Перпендикулярная
ей составляющая потокосцепления, пронизывающая плоскость витков обмотки, как
известно из курса электротехники, не будет наводить в витках данной обмотки
ЭДС вращения. Поэтому в обмотке d, а следовательно, и в уравнении
относительно
обмоток статора, в каждой из них наводится ЭДС вращения. Величина ЭДС вращения
пропорциональна произведению скорости перемещения на составляющую
потокосцепления, направленную вдоль плоскости данной обмотки. Перпендикулярная
ей составляющая потокосцепления, пронизывающая плоскость витков обмотки, как
известно из курса электротехники, не будет наводить в витках данной обмотки
ЭДС вращения. Поэтому в обмотке d, а следовательно, и в уравнении ![]() появляется ЭДС вращения
появляется ЭДС вращения ![]() , а в обмотке q и в уравнении
, а в обмотке q и в уравнении ![]() – ЭДС
вращения
– ЭДС
вращения ![]() .
.
Следует
обратить внимание, что при физическом истолковании преобразований Парка – Горева
обмотку статора необходимо полагать неподвижной, вращается только система
токов ![]() . Если предположить обмотку
вращающейся, то тогда исчезает ЭДС вращения. Поэтому правильное представление
получается, когда считаем, что обмотки статора неподвижны, а вращаются
воображаемые щетки, как показано на рис. 1.10.
. Если предположить обмотку
вращающейся, то тогда исчезает ЭДС вращения. Поэтому правильное представление
получается, когда считаем, что обмотки статора неподвижны, а вращаются
воображаемые щетки, как показано на рис. 1.10.
Для анализа переходного процесса синхронной машины систему уравнений напряжений статора (1.27) необходимо дополнить уравнением (1.3) для обмотки возбуждения. Тогда полная система уравнений
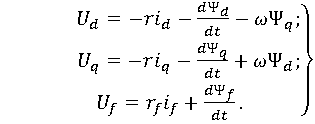 (1.28)
(1.28)
На
модели синхронной машины (рис. 1.10) наглядно можно получить выражение для
электромагнитного момента. Известно, что в машинах переменного тока
электромагнитный момент равен произведению тока в обмотке статора,
потокосцепления и синуса угла между ними. Исходя из данного положения и
известного «правила левой руки», на рис. 1.10 можно установить, что действующие
на ротор электромагнитные силы от взаимодействия одноименных токов и потокосцеплений
обмотки статора (![]() ) равны нулю, т. е.
) равны нулю, т. е.![]() и
и ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.