Многоцикловое и истирающее воздействия дрейфующего ледяного покрова на морские гидротехнические сооружения (Расчет конструкции ледостойких оснований. Особенности имитационного моделирования), страница 7

Описание блока А.

Законы распределения величины А при известных А_min и А_max строится следующим образом. Вычисляем значение DА=(А_max-А_min)/N_a (здесь N заранее заданное значение числа разбиения промежутков). Тогда частота попадания величины в определенный промежуток [А_min+(k-1)×DА, А_min+kDА] определяется числом ее попаданий А_k деленный на общее число испытаний .

Принятые допущения к модели.

1. Все величины в модели являются независимыми случайными величинами.

2. Значение ледовой нагрузки определяется по формуле :

,                                                                    (     )

где k - коэффициент формы опоры; D - диаметр сооружения в зоне контакта со льдом; h - толщина льда; R - нормативное сопротивление льда одноосному сжатию.

3. Скорость относительных деформаций e льда в зоне контакта с сооружением определяется по формуле:

,                                                                        (     )

4. Зависимость прочности льда на одноосное сжатие от скорости его деформирования принята в виде:

,                                                               (    )

где a, b - параметры аппроксимации;

-при e<10^-3, a=11.85 МПа; b=1.45

-при 10^-3<e<10^-2, a=-1.5 МПа; b=-3

-при e<10^-2, a=4.5 МПа; b=0

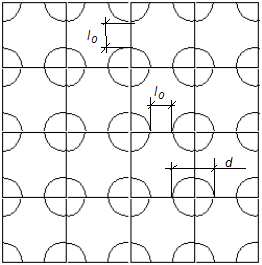
5. Льдины приняты круглые в плане и распределены равномерно по рассматриваемой площади с шириной квадрата а (см.рис.   )

5.1. Опора сооружения и льдины соосны в плане .

5.2. Первоначальное расстояние между льдинами одинаково.

Вывод формулы для расчета расстояния между льдинами.

Пусть Q - сплоченность льда в данном районе. Известно, что сплоченность -есть отношение площади акватории, занятой льдом (S₁), к площади рассматриваемого района (S₂):

,                                                                       (     )

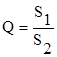следовательно:

,                                                                        (   )

Обозначим сторону квадрата (района) - а и а₁- сторону квадрата, площадь которого занял бы весь лед данного района без пробелов (рис.     ).

 

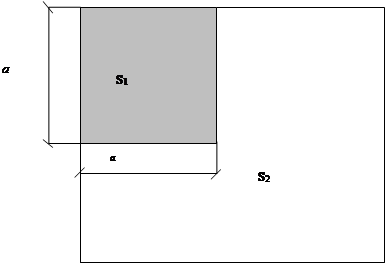Рис. I

Тогда:

,                                                  (   )

Число льдин в заданном районе выразится следующим образом:

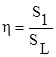,                                                                      (I)

где S_L - площадь льдины.

Так как льдины приняты круглые (см. допущение 5), то при известном диаметре d имеем:

,                                                                 (    )

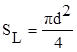следовательно формула (I) примет вид:

,                                                                       (   )

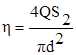При наиболее равномерном распределении по квадрату все льдины располагаются в узлах сетки (2). Поэтому количество льдин по вертикали и по горизонтали одинаково и равно . Так как (a-a₁) - это общая длина промежутков между льдинами, находящими на одной линии по вертикали (или по горизонтали), то расстояния между двумя любыми соседними льдинами:

,                                                                    (   )

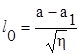Путем использования ранее приведенных выражений (     ) и математических преобразований, получим:

,                                                                 (    )

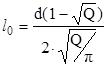6. Локальная зона напряженно-деформируемого состояния льда на контакте равна 2d=B_min.

	Рис. 2. Схема расположения льдин в квадрате

 

7. При определении кинетической энергии льдин не учитывается масса скалывающегося в процессе прорезания льда и присоединенной воды.

8. Граница скалывающейся массы проходит по прямой перпендикулярной оси движения льда через переднюю точку конструкции.

9. Период нагружения определяется по формуле Маатанена:

,                                                                           (   )

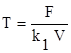где k₁ - коэффициент жесткости.

10. В данной модели принята схема разрушения ледяного покрова в зоне контакта сколом со смятием.