По существу, при вероятностном подходе определяется совокупность возможных режимов эксплуатации сооружения. Такая совокупность характеризуется распределением многомерной случайной величины X (Rc, Rf, t), каждый из аргументов которой также является случайной величиной. Тогда расчет ледовой нагрузки на сооружение F сводится к определению одномерной функции распределения
![]() (1,2)
(1,2)
где f(x) - случайная функция параметров, определяющих величину ледовой нагрузки на данное сооружение. Функция f(x) определяется особенностями непосредственно силового контакта льда с сооружением и формой разрушения при заданной величине Х. Иными словами F=f(x) - детерминированная ледовая нагрузка, соответствующая конкретному режиму эксплуатации Х.
Функция Ф(Х) определяется по данным натурных наблюдений. В простейших случаях принимается гипотеза статистической независимости всех случайных величин, Ф(Х)=Ф(Rc)Ф(Rf). Так, например, при определении ледовой нагрузки F при прорезании ледяным покровом отдельно стоящей опоры вероятность уровня нагрузки определяется по формуле:
![]() (1,3)
(1,3)
Основная практическая сложность заключается в численном определении вероятностей всех входящих в формулу величин.
Недостаточность исходных данных вынуждает к предельным упрощениям вероятностной модели. Поэтому обычно вводится гипотеза статистической независимости почти всех случайных величин, участвующих в процессе взаимодействия ледяного поля с сооружением. С помощью такой упрощенной задачи в работе разработан алгоритм определения режима нагружения ледяным покровом.
В работе создана имитационная модель определения ледовых нагрузок на сооружения за весь период эксплуатации.
Исходными данными для расчета являются: параметры сооружения, толщина h, средняя скорость дрейфа ровного ледяного покрова для различных направлений V, прочность льда R с учетом температуры и солености, продолжительность ледового периода ts, размер льдин R, сплоченность льда N.
Для исследования режима нагружения ровного ледяного покрова на конструкции гидротехнических сооружений учитываются следующие факторы: геометрические (толщина h и сплоченость N льда, средние размеры b, разрушенность льдин и т.д.), прочностные (прочность льда на изгиб Ri и сжатие Rs и т.д.), кинематические (скорость дрейфа v и скорость деформации e) ледяного покрова.
Для описания рассматриваемого явления был использован язык теории вероятности и математической статистики. Соответствующим образом используются случайные величины, их плотности вероятности p и законы распределения P. Последние связаны выражением:
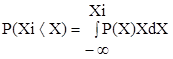 (1.5)
(1.5)
Для оценки характеристик внешних нагрузок использовалась совместная плотность распределения скорости дрейфа и толщины льда p(vi<v, hi<h). Плотность распределения прочности p(Ri<R) зависит от скорости деформации , которая в свою очередь зависит от скорости дрейфа льда. Следовательно, плотность распределения скорости деформации совпадает с плотностью распределения скорости дрейфа p(ei<e)=p(vi<v), тогда
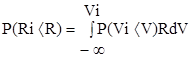 (1.7)
(1.7)
а интегральный закон распределения ледовой нагрузки F имеет вид
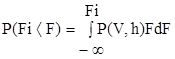 (1.8)
(1.8)
Поскольку прочность льда прямо пропорционально зависит от скорости деформации (допущение 3), которая в свою очередь прямо пропорционально зависит от скорости деформации льда e/, что обусловливает совпадение плотности распределения скорости деформации р(e/i<e/) c плотностью распределения скорости дрейфа льда p(vi<v), т.е.
![]() ,
( )
,
( )
тогда интегральный закон распределения прочности льда запишется в виде
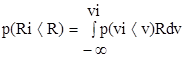 (
)
(
)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.