Многоцикловое и истирающее воздействия дрейфующего ледяного покрова на морские гидротехнические сооружения (Расчет конструкции ледостойких оснований. Особенности имитационного моделирования), страница 10

где x=x(t) - глубина внедрения; r=r(x,t) - плотность льда; M - масса и V - cкорость движения льдины до соприкосновения с опорой гидротехнического сооружения; v=v(x,t) - скорость движения льдины с момента соприкосновения льдины с опорой до полной ее остановки; h=h(x,t) - ее толщина и A - общая площадь; расчетное значение контактной силы определяется выражением Р(х,t)=2vh(rAR_b)^1/2 [5], где R_b - прочность льда на смятие. Решение интегрального уравнения позволяет оценить только максимальную глубину внедрения ледяной плиты в опору ледостойкого основания, а вопрос об оценке времени внедрения остается открытым. Между тем, именно величина временного интервала необходима для разработки имитационных моделей изучаемых объектов. Особо следует подчеркнуть отсутствие методики решения (1), являющегося математической формализацией балансового соотношения.

Рассмотрим упрощенный случай когда при постоянных значениях плотности r=const и толщины h=const скорость внедрения является только функцией времени v(x,t)=v(t). В этой ситуации предлагается следующий аналитический способ решения (1). Прежде всего заметим, что dx=vdt. При этих условиях (1) трансформируется следующим образом 

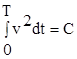,                                                                (2)

где C=(MV²/2)/[ 2h(rAR_b)^1/2] и T - время окончания процесса внедрения льдины, значение же величины внедрения определяется выражением

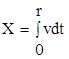                                                                  (3)

Далее конкретизируем вид функции v исходя из того факта, что он должен соответствовать профилю монотонно убывающей функции на участке от 0 до T - промежутку времени от момента соприкосновения льдины с опорой до ее полной остановки. Параметры подбираются таким образом, что v(0)=V и v(T)=0. Предлагаются следующие модели, удовлетворяющие данным условиям:

1. 

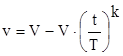
2. 

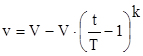
где k - некоторое целое четное число. Различие этих функций состоит в том, что первая из модификаций есть выпуклая функция, а вторая - вогнутая. Таким образом, во втором случае скорость стремится к нулю быстрее нежели в первом случае; степень стремления к нулю характеризуется числом k. Подставив выражения для v в (2) и (3) получим следующие значения глубины внедрения X и времени внедрения T льдины в опору ледостойкого основания от момента начального контакта до ее полной остановки

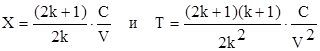                                                       (4)

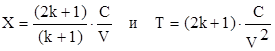                                                                (5)

Сравнительный анализ полученных выражений показывает, что при выборе первой модели глубина внедрения льдины меньше нежели глубина внедрения при выборе второй модели, а время внедрения для первой модели скорости больше соответствующего времени для второй модели.

Рассмотрим теперь ситуацию для которой льдины сначала накапливаются перед опорой ледостойкого основания, а затем, по мере роста интегральной силы навала на опору, имеет место процесс их внедрения. Сила навала F_s остановившегося ледяного поля на опору ледостойкого основания пропорциональна площади ледяного поля A и согласно [6] определяется формулой

,                                                   (6)

где p₁=5×10^-6v²_m - напряжение трения, вызванное течением воды, v_m - максимальная скорость течения воды подо льдом 1 % обеспеченности, м/с; p₂=5×10^-4hv²_m/L - нагрузка от воздействия течения воды на торец льдины, L - средняя длина ледяного поля по направлению потока, м; p₃=9.2×10^-3h×i - нагрузка, вызванная уклоном i поверхности потока (поскольку в настоящей работе рассматриваются морские гидротехнические сооружения, то i=0); p4=2×10^-8×v²_w - напряжение трения ветра, v_w - максимальная скорость ветра 1 % обеспеченности, м/с. Легко показать [5], что основной вклад в нагрузку от ледяного поля обеспечивает воздействие ветра. Там же приводятся рекомендации для численной оценки скорости ветра v_w. Сформулируем теперь основные балансовые соотношения, которым подчиняются отдельные компоненты системы «остановившееся ледяное поле - опора ледостойкого основания». Пусть X - глубина внедрения. Тогда F_s×X - работа, которую выполняет ледяное поле при его внедрении. Совершено очевиден факт ее расхода на разрушение объема ледяного тела, высота которого равна толщине льда h и площадью основания S, равной площади зоны внедрения опоры в лед (диссипацией внутренней энергии этого тела в силу ее малости можно пренебречь). Таким образом, мы получаем следующее энергетическое балансовое соотношение: