а интегральный закон распределения ледовой нагрузки p(Fi<F) примет вид:
,
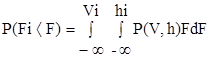(1.9)
где p(v,h)=p(vi<v)×p(hi<h), т.к. толщина и скорость дрейфа льда являются взаимонезависимыми величинами (допущение 1)
Скорость деформации определяется выражением e/=v/2d, гдеv - скорость дрейфа, d - диаметр сооружения.
Cкорость деформации зависит от скорости дрейфа льда. Поэтому плотность распределения прочности льда р(Ri<R) совпадает с плотностью распределения скорости дрейфа p(vi<v) и указанная совместная плотность распределения р(hi<h,vi<v) характеризует вероятностное описание процесса, о чем говорилось ранее. Поскольку, толщина льда не зависит от скорости дрейфа, то функция р(hi<h,vi<v) равна произведению одномерных функций плотностей распределения толщины льда и скорости дрейфа льда.
,
(1.10)
т.к. толщина и скорость дрейфа льда независимые случайные величины.
Поэтому используются случайные величины, их плотности распределений и соответствующие законы распределения случайных величин.
Предложенная методика была использована для моделирования закона распределения прочности льда, где мы полагаем, что прочность льда распределена по логнормальному закону и является функцией скорости деформации, скорости дрейфа льда, его солености и температуры. Здесь выбор именно этого распределения обусловлен следующими особенностями самого логнормального распределения: значение логарифмически нормальной величины формируется под воздействием очень большого числа взаимно независимых факторов, причем воздействие каждого отдельного фактора «равномерно незначительно» и равномерно по знаку (т.е. воздействие равномерно по всем направлениям и каждое последующее воздействие не зависит от предыдущего), а случайный прирост, вызываемый действием каждого следующего фактора, пропорционален уже достигнутому к этому моменту значению исследуемой величины [7]. Ее среднее значение определяется с учетом зависимости скорости деформации льда от прочности льда. Дисперсия прочности определяется с использованием натурных данных. Далее, при наших допущениях и численной оценки силы действия ледовых полей на отдельно стоящие опоры при прорезании ими льда F [8], мы можем получить закон ее распределения. Количественное определение силы имеет вид:
(1,11)
где m- коэффициент формы опоры.
Учитывая, что характер разрушения ледяных полей у сооружения в большинстве случаев носит хрупкий характер, нагрузка имеет циклический характер, поэтому с позиции усталостного описания процесс взаимодействия ледяного покрова и сооружения описывается режимом нагружения. Режим нагружения сооружения характеризуется связью между уровнем нагрузки и количеством циклов нагружения. Здесь и далее термин “цикл нагружения” численно характеризует время между началом роста нагрузки и ее сколом. Тогда “количество циклов нагружения” - это общее число пиков нагрузки льда на сооружение. Количество циклов нагружения N сооружения ледяным покровом на каждом этапе нагружения имеет вид
(1,12)
где ti - время действия каждого фиксированного уровня нагрузки при фиксированной толщине и прочности льда, P(Ti) - вероятность возникновения этого фиксированного уровня; ts - длительность ледового периода; Ti - период циклического колебания нагрузки.
Общее количество циклов нагружения сооружения дрейфующим ледяным покровом за весь период эксплуатации сооружения составит:
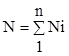(1,13)
где i=[1; n], n - количество выделенных уровней нагрузки.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.