Многоцикловое и истирающее воздействия дрейфующего ледяного покрова на морские гидротехнические сооружения (Расчет конструкции ледостойких оснований. Особенности имитационного моделирования), страница 11

,                                                      (7)

где E₀- удельная энергия разрушения. Последняя оценивается по энергии удара, отнесенной к объему разрушенного льда. Численные оценки E₀ приводятся в [7]. Левая часть (4) является количественной оценкой работы, которую надо выполнить, чтобы разрушить ледяное тело с площадью основания S и высотой h. В первом приближении зона внедрения представляет собой сектор окружности радиуса r_c. Легко показать, что в этом случае площадь зоны внедрения определяется выражением S=r²_c[p/2-arcsin(y)+y(1-y²)^1/2]. Переменная y принимает значение (r_c-X)/r_c при X<r_c и (X-r)/r_c в противном случае. Учитывая вышесказанное, перепишем уравнение (7) следующим образом

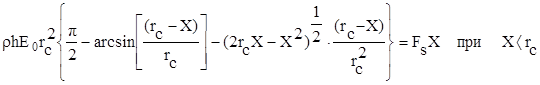           (8)

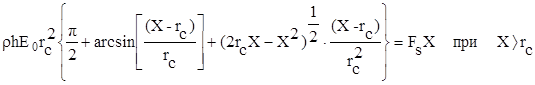           (9)

Легко заметить, что в разумном диапазоне изменения XÌ[0,2r_c] для этих уравнений справедливы утверждения.

·  При низких значениях силы навала F_s уравнения (8) и (9) имеют ровно один корень X=0 (отсутствие внедрения) и перед опорой ледостойкого основания происходит аккумуляция льда;

·  При высоких значениях силы навала F_s уравнения (8) и (9) имеют два корня, один из которых является оценкой глубины внедрения опоры ледостойкого основания в льдину.

Поскольку (8) и (9) существенно нелинейны, то для их решения следует использовать тот или иной способ решения нелинейных уравнений и, кроме того, задать начальное приближение. Понятно, что при создании эволюционной модели требуется указать простой и надежный способ решения этих уравнений. Для его реализации можно предложить следующий алгоритм:

1.  Промежуток [0,2 r_с] делится на равные части и для каждого x_i=i×r_c/N (i=1¸N) вычисляются левые и правые части (8) и (9);

2.  Корнем уравнения X считается то значение x_i, где с заранее заданной степенью точности (очевиден факт зависимости этой величины от значения N) левые и правые части этих уравнение совпадают.

Таким образом, число корней уравнения определяется критическим значением работы A_c (X): если F_s×X₁< A_c (X₁), то (8) имеет ровно один корень X=0 и прорезание отсутствует.

Для вычисления времени окончания процесса внедрения следует воспользоваться (3). Так же как и в предыдущем случае определим идентичные модели скоростей внедрения:

1. 

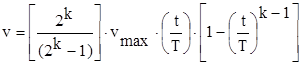
2. 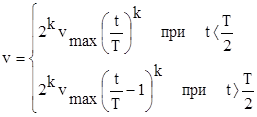 , где k некоторое целое четное число, отражающее степень стремления к нулю скорости внедрения; v_max - максимальная скорость внедрения для рассматриваемого процесса (оценивается по натурным данным); T - подлежащее определению время окончания процесса внедрения льдины в сооружение. Согласно этим моделям, при превышении силы навала некоторого критического значения имеет место процесс внедрения ледяного поля в опору. При этом сначала происходит рост скорости внедрения, а затем убывание ее до нуля. Подставляя выражения для скоростей в (3) и опуская математические выкладки, получим

1. 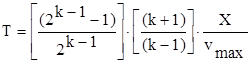                                                     (10)

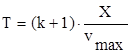2.                                                                                  (11)

Подобно аналогичным величинам для предыдущего случая, сравнительный анализ полученных выражений показывает, что при выборе первой модели глубина внедрения льдины меньше нежели глубина внедрения при выборе второй модели, а время внедрения для первой модели скорости больше соответствующего времени для второй модели.