Нормирование расчетных параметров для проектирования строительных конструкций: Методические указания к практическим занятиям по дисциплине "Вероятностные методы расчета строительных конструкций", страница 7

На основании полученной величины гарантированного с вероятностью в 95 % нормативного сопротивления устанавливается класс бетона или арматурной стали по табл. 12, 19, 20 [СНиП 2.03.01-84(1996) Бетонные и железобетонные конструкции].

5.2. Определение нормативных и расчетных сопротивлений бетона

С учетом изложенного выше, класс бетона B (нормативное сопротивление осевому сжатию бетонных кубов) можно определить по одной из формул: B = R_m - a_R×S,  или   B = R_m×(1 - a_R×V).

Нормативное сопротивление осевому сжатию бетонных призм R_bn (нормативная призменная прочность) определяется по формуле

R_bn = B×(0.77 - 0.001×R_m) и принимается не менее 0.72B.

Нормативное сопротивление бетона осевому растяжению можно приближенно определить по формуле:

.

Расчетные сопротивления бетона осевому сжатию и осевому растяжению определятся, соответственно, по формулам:

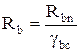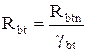; , где коэффициент надежности по бетону при сжатии  g_bc = 1.3, коэффициент надежности по бетону при растяжении g_bt = 1.5.

Аналогичные расчеты необходимо выполнить для усредненного коэффициента вариации прочности бетона V = 0.135.  Для этого случая класс бетона B определится по формуле B = R_m×(1 - a_R×V) = R_m×(1 - 0.135×a_R), а нормативные и расчетные сопротивления бетона - по приведенным выше формулам.

Результаты вычислений нужно свести в таблицу (см. табл. 8). Кроме этого в нее следует записать прочностные характеристики для ближайшего к полученному вами на основании статистической обработки результатов испытаний классу бетона, принятого по табл. 12 [СНиП 2.03.01-84(1996) Бетонные и железобетонные конструкции].

Таблица 8

n	B	Rbn	Rbtn	Rb	Rbt
…. 0.135
СНиП

На основании данных табл. 8  необходимо выполнить анализ полученных результатов и сделать выводы.

5.3. Определение нормативных и расчетных сопротивлений

арматурной стали

Нормативные сопротивления стержневой арматуры, высокопрочной проволоки и арматурных канатов осевому растяжению R_sn принимаются равными наименьшему контролируемому значению предела текучести (физического или условного) с гарантированной вероятностью 95 % (g = 0.95) и определяются по формулам:

R_sn = R_m - a_R×S,     или    R_sn = R_m×(1 - a_R×V).

Расчетные сопротивления арматуры растяжению R_s для предельных состояний первой группы определяются по формуле

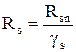, где g_s - коэффициент надежности по арматуре, принимаемый по табл. 21 [СНиП 2.03.01-84(1996) Бетонные и железобетонные конструкции].

Расчетные сопротивления арматуры осевому сжатию R_sc, используемые при расчетах конструкций по предельным состояниям первой группы, принимаются равными соответствующим расчетным сопротивлениям арматуры растяжению R_s, но не более 400 МПа.

Расчетные сопротивления растяжению поперечной арматуры R_sw определяются по формуле

R_sw = R_s×g_s1×g_s2 , где g_s1 и g_s2 - коэффициенты условий работы,  принимаемые в соответствии с требованиями п. 2.28 [СНиП 2.03.01-84(1996) Бетонные и железобетонные конструкции].

Аналогичные расчеты необходимо выполнить для усредненного коэффициента вариации прочности арматурной стали V = 0.05.

Результаты вычислений нужно свести в таблицу (см. табл. 9). Кроме этого в нее следует записать прочностные характеристики для ближайшего к полученному Вами на основании статистической обработки результатов испытаний классу арматуры, принятому на основании данных табл. 19 и 20 [СНиП 2.03.01-84(1996) Бетонные и железобетонные конструкции].

Таблица 9

n	Rsn	Rs	Rsc	Rsw
... 0.05
СНиП

На основании данных табл. 9 выполните анализ полученных результатов и сделайте выводы о том, факторы влияют в данном случае на установленные Вами прочностные характеристики арматуры и каким образом проявляется в данном конкретном случае это влияние.