Строительство и архитектура \ Вероятностные методы расчета строительных конструкций

Нормирование расчетных параметров для проектирования строительных конструкций: Методические указания к практическим занятиям по дисциплине "Вероятностные методы расчета строительных конструкций", страница 4

Если выборочный коэффициент асимметрии A* < 0, то имеет место левосторонняя асимметрия статистической (эмпирической) функции плотности распределения вероятности, то есть слева от математического ожидания прочности будет сосредоточена большая масса. Если A* > 0, то соответственно имеет место правосторонняя асимметрия.

Если выборочный коэффициент эксцесса E* < 0, то график функции плотности вероятности менее крутой и имеет более плоскую вершину, чем нормальная кривая с теми же математическим ожиданием и дисперсией. Если E* > 0, то график функции плотности вероятности более крутой по сравнению с нормальной кривой и имеет более острую вершину.

Промежуточные вычисления, необходимые для определения параметров статистического распределения, удобно выполнять в табличной форме (см. табл. 4).

Таблица 4

Середины интервалов

Rmi

Частоты,

ni

Rmi × ni

(Rmi - Rm)

(Rmi - Rm)2×ni

(Rmi - Rm)3×ni

(Rmi - Rm)4×ni

Rm1

n1

Rm1 × n1

(Rm1- Rm)

(Rm1 - Rm)2×n1

(Rm1 - Rm)3×n1

(Rm1 - Rm)4×n1

…..

…..

…..

…..

…..

…..

…..

Rm9

n9

Rm9 × n9

(Rm9- Rm)

(Rm9 - Rm)2×n9

(Rm9 - Rm)3×n9

(Rm9 - Rm)4×n9

n

SRmi × ni

S(Rmi -Rm)

S(Rmi - Rm)2×ni

S(Rmi - Rm)3×ni

S(Rmi - Rm)4×ni

2.2. Приближенная проверка нормальности распределения

О близости статистического (эмпирического) распределения к нормальному можно судить по величине выборочных коэффициента асимметрии A* и коэффициента эксцесса E*. Для нормального закона распределения случайной величины  A = 0 и E = 0.

О том, насколько малы выборочные (эмпирические) характеристики, можно судить по сравнению величин E* и A* с их средними квадратическими ошибками, равным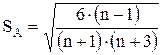и

 и 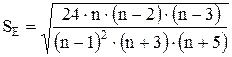 , где  n - объем выборки.

Если выполняются неравенства

|A*| £ 3×SA   и   |E*| £ 3×SE, то это является основанием для выдвижения гипотезы о нормальности закона распределения исследуемой случайной величины.

2.3. Построение функции плотности распределения вероятности

После определения выборочных оценок статистического (эмпирического) распределения и приближенной проверки гипотезы о нормальности распределения на графике с гистограммой строят гипотетическую (предполагаемую) функцию плотности распределения вероятности. В основе такой статистической функции лежит ф-ла нормального распределения Гаусса:

.

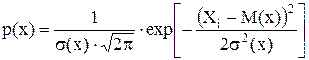В качестве неизвестных параметров выбранного закона распределения берутся их выборочные оценки, то есть считается, что математическое ожидание M(R) = Rm, среднее квадратическое отклонение s(R) = S, а дисперсия s2(R) = S2. Вычисление промежуточных значений функции плотности вероятности по интервалам удобно выполнять в табличной форме (см. табл. 5).

Таблица 5

M(R) = Rm = ________ МПа, s(R) = S = ________ МПа.

Середины интервалов Rmi

(Rmi - Rm)

p(R)

Rm1

(Rm1- Rm)

p1(R)

…..

…..

…..

…..

…..

…..

Rm9

(Rm9- Rm)

p9(R)

Практическая работа № 3

Определение доверительных интервалов параметров статистического распределения

3.1. Доверительные интервалы

Поскольку выборочные оценки параметров статистического распределения носят приближенный характер, они могут существенно отличаться от оцениваемого параметра. Чтобы дать представление о точности и надежности выборочной оценки, строят так называемые доверительные интервалы.

Скачать файл