Нормирование расчетных параметров для проектирования строительных конструкций: Методические указания к практическим занятиям по дисциплине "Вероятностные методы расчета строительных конструкций", страница 3

Для построения интервального вариационного ряда весь диапазон наблюдаемых значений случайной величины делится на ряд интервалов равной длины. Для определения оптимальной длины интервала h обычно используют формулу Стерджеса:

.

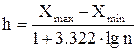При значении  n = 100 знаменатель формулы будет равен 7.644.  Для разбивки на интервалы одинаковой длины его округляем до 8. Тогда формула Стерджеса для определения длины интервала примет вид:

.

За начало первого интервала принимают величину , а границы второго, третьего и последующих интервалов определяют по формуле a_i = a_i-1 + h, где i = 2, 3, ….. , 10. Конец последнего интервала в этом случае будет равен , а количество интервалов при таком разбиении будет равно 9.

Выборочные значения непрерывно изменяющейся в пределах интервала случайной величины заменяют дискретным значением, равным середине интервала: , (i = 1, 2, 3, ….. , 9), то есть полагают, что все попавшие в данный интервал значения непрерывной случайной величины равны R_mi.

После этого подсчитывают число значений случайной величины, попавших в каждый интервал (частоту) n_i. Значение случайной величины, попавшее на границу интервалов, принято относить к интервалу с меньшим номером.

Затем вычисляют относительную частоту w_i по формуле , где  n_i - число выборочных значений, попавших в интервал (a_i, a_i+1) и определяют для каждого интервала отношения w_i/h, необходимые для построения гистограммы.

1.3. Построение гистограммы

Для выдвижения гипотезы о законе распределения случайной величины строится полигон относительных частот (для дискретной случайной величины) или гистограмма (для непрерывной случайной величины). Поскольку в диапазоне наблюдаемых значений прочность строительных материалов изменяется непрерывно, для выдвижения гипотезы о законе распределения прочности необходимо построить гистограмму.

Гистограмма строится в осях и представляет из себя ступенчатую фигуру, состоящую из прямоугольников, основания которых - интервалы длины h, а высоты равны w_i/h. Таким образом, площадь каждого прямоугольника гистограммы равна относительной частоте значений случайной величины, а полная площадь всей гистограммы будет равна 1. Вид гистограммы показан на рис. 1.

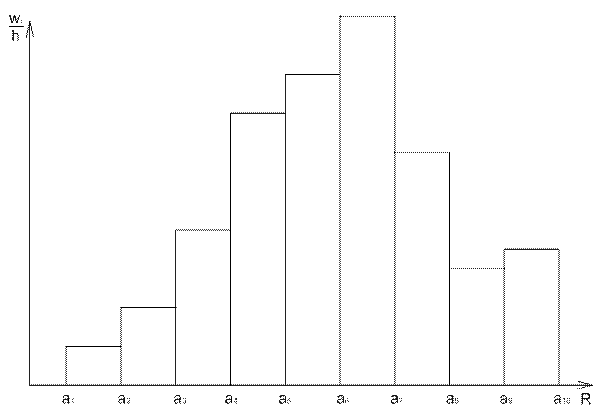
Рис. 1. Гистограмма распределения прочности материала

При одновременном увеличении числа наблюдений случайной величины n и уменьшении длин интервалов h контур гистограммы приближается к графику функции распределения плотности вероятности непрерывной случайной величины, что позволяет сделать предварительный вывод о законе ее распределения.

Практическая работа № 2

Определение  параметров  статистического  распределения  и построение  функции  плотности  распределения  вероятности

2.1. Определение параметров статистического распределения

После выдвижения гипотезы о законе распределения случайной величины возникает необходимость в определении основных параметров выбранного закона распределения. Поскольку статистическое (эмпирическое) распределение случайной величины не обязательно полностью совпадает с теоретическим распределением, параметры статистического распределения носят приближенный характер и часто называются выборочными оценками параметров теоретического распределения.

Выборочное среднее, как оценку для математического ожидания теоретического распределения прочности строительного материала, можно определить по формуле:

.

Выборочную дисперсию, как оценку для дисперсии теоретического распределения прочности, определяют по формуле:

.

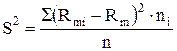Тогда среднее квадратическое отклонение прочности (или стандарт) определится по формуле:

, а коэффициент вариации прочности - по формуле:

.

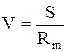Далее необходимо определить выборочный коэффициент асимметрии

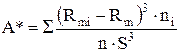
и выборочный коэффициент эксцесса

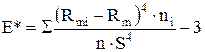
как оценки  для  коэффициента асимметрии A и коэффициента эксцесса E теоретического распределения.