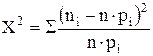Нормирование расчетных параметров для проектирования строительных конструкций: Методические указания к практическим занятиям по дисциплине "Вероятностные методы расчета строительных конструкций", страница 6

, где i = 1,  2, ..., k, при больших n практически не зависит от гипотетического распределения и имеет распределение X² с степенями свободы. 

Число степеней свободы r = k - m - 1, где  m - количество неизвестных параметров статистического распределения, оцениваемых по выборке. Для нормального распределения такими параметрами являются  R_m и s(R), то есть m = 2.

Чтобы проверить принятую гипотезу о виде закона распределения случайной величины R, следует выбрать уровень значимости b = 1 - g. Затем по Приложению 3 в зависимости от уровня значимости b и числа степеней свободы r найдем такое число , чтобы выполнялось равенство .

4.2. Практическое применение критерия Пирсона

В первую очередь по приведенной выше формуле вычисляется выборочное значение X². Данные вычисления удобно вести в табличной форме, фиксируя промежуточные результаты (см. табл. 6). Учтите при этом, что каждый интервал вносит в X² вклад, равный ,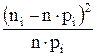  

где n×p_i - число попаданий в i-ый интервал.

При малых значениях n×p_i (в начале и в конце диапазона изменения случайной величины R) роль каждого отдельного наблюдения становится велика. Чтобы ее снизить, рекомендуется сделать разбивку на интервалы так, чтобы все n×p_i были достаточно большими. На практике это сводится к требованию иметь в каждом интервале не менее 5-10 наблюдений. Для этого интервалы, содержащие мало наблюдений, рекомендуется объединять с соседними.

Вероятность того, что случайная величина R примет значение, принадлежащее интервалу (a_i; a_i+1), можно определить по формуле:

.

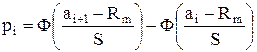Значения функции  Ф(x)  вычислены и сведены в таблицу (см. Приложение 4). При этом следует учесть, что Ф(-x) = 1 - Ф(x).

Таблица 6

Далее определяется уровень значимости b (при g = 0.95), число степеней свободы r и по Приложению 3 находится критическое значение .

Если значение X², вычисленное на основании статистической выборки, окажется больше или равно , то гипотезу о законе распределения случайной величины отвергают.  Если же выборочное значение X² < , то гипотезу о законе распределения принимают, то есть считают, что выдвинутая гипотеза не противоречит опытным данным.

Практическая работа № 5

Определение нормативных и расчетных сопротивлений материалов

5.1. Определение нормативных сопротивлений

Нормативное сопротивление материалов назначается на основании статистической обработки результатов испытаний образцов и принимается равным гарантированному с доверительной вероятностью 95 % (g = 0.95) минимальному значению прочности, определяемому по формуле:

R_n = R_m - a_R×s(R), где a_R - коэффициент (число стандартов прочности), учитывающий объем испытаний и гарантированную обеспеченность результатов с вероятностью 0.95, определяемый по табл. 7; s(R) - среднее квадратическое отклонение теоретического распределения прочности.

Поскольку среднее квадратическое распределение (стандарт) теоретического распределения нам неизвестно, в практических расчетах используют эмпирическое (выборочное) среднее квадратическое отклонение S.

Таблица 7