Нормирование расчетных параметров для проектирования строительных конструкций: Методические указания к практическим занятиям по дисциплине "Вероятностные методы расчета строительных конструкций", страница 5

Пусть X* - выборочная оценка для параметра X. Зададим достаточно большую вероятность g (например, g = 0.9; 0.95; 0.99) и найдем такое e > 0, для которого p(|X - X*| < e) = g или, что то же самое,

p(X* - e < X < X* + e) = g.

Последнее означает, что с вероятностью g неизвестное значение параметра X находится в интервале (X* - e; X* + e).

Такой интервал называется доверительным интервалом, число g называется надежностью или доверительной вероятностью, число b = 1 - g называется уровнем значимости, а  e - точностью оценки.

3.2. Определение доверительного интервала для математического

        ожидания случайной величины

Выборочной оценкой для математического ожидания прочности M(R) служит выборочное среднее R_m, следовательно, доверительный интервал для M(R) имеет вид (R_m - e; R_m + e).

Задавая надежность g = 0.95, подберем e так, чтобы выполнялось соотношение p(|R_m - M(R)| < e) = g.

При определении доверительного интервала для математического ожидания прочности возможны два случая: когда дисперсия нормальной случайной величины s(R) известна и когда дисперсия случайной величины неизвестна.

В нашем случае дисперсия неизвестна. Тогда воспользуемся тем, что случайная величина

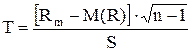
имеет распределение Стьюдента с (n -1) степенями свободы.

Найдем такое число t_g, что  p(|T| < t_g) = g.

Последнее равенство означает, что

.

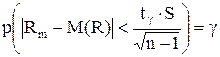Далее по заданному уровню надежности  b и  числу степеней свободы  n  по Приложению 1 найдем такое число t_g, что p(|T| > t_g) = b = 1 - g. Следовательно, искомый доверительный интервал будет иметь вид (R_m - e; R_m + e), где .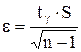

3.3. Определение доверительного интервала для неизвестной

дисперсии случайной величины

Выборочными оценками для дисперсии прочности s²(R) служит S², а для среднего квадратического отклонения прочности s(R) - S.

При построения доверительных интервалов дисперсии и среднего квадратического отклонения пользуются тем, что случайная величина имеет распределение хи-квадрат (распределение Пирсона), то есть 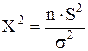. Для определения границ доверительных интервалов с надежностью g = 0.95 по Приложению 2 при числе степеней свободы n - 1 необходимо найти числа g₁ и  g₂.

Тогда искомый доверительный интервал для дисперсии прочности s²(R) будет равен , а для среднего квадратического отклонения прочности s²(R) - .

Практическая работа № 4

Проверка гипотезы о законе распределения исследуемой случайной величины

4.1. Критерий согласия Пирсона

Под статистической гипотезой понимают всякое предположение о распределении исследуемой случайной величины, проверяемое на основании имеющейся выборки. Для проверки статистических гипотез используют статистические критерии - правила, указывающие, когда статистическую гипотезу следует принять, а когда отвергнуть. Критерии, относящиеся исключительно к виду функции распределения или к виду плотности распределения вероятности исследуемой случайной величины, называются критериями согласия.

Наиболее употребительным критерием согласия является критерий хи-квадрат или критерий Пирсона (по имени его автора, английского математика К. Пирсона, одного из основоположников математической статистики). Его название связано с используемой в нем статистикой (оценкой), которую обозначают X², а также распределением X².

Пусть вся область изменения случайной величины R, подчиняющейся какому-либо закону распределения, разбита на k интервалов (a₁; a₂), (a₂; a₃), ....., (a_k; a_k+1)  и p_i - вероятность того, что случайная величина R примет значение, принадлежащее интервалу (a_i; a_i+1), то есть

p_i = p(a_i < R £ a_i+1).

Пусть также n_i - число выборочных значений случайной величины R, попавших в интервал (a_i; a_i+1), где i = 1, 2, ..., k, а n - объем выборки.

Если величины n_i/n и p_i, (i = 1, 2, ..., k), мало различаются, то разумно считать, что выдвинутая гипотеза о законе распределения случайной величины не противоречит опытным данным. Это обстоятельство и положено в основу критерия хи-квадрат (X²) или критерия Пирсона.

Доказано, что статистика (оценка)