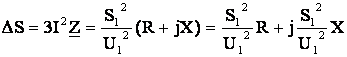Расчет режимов разомкнутых электрических сетей, страница 3

.                                      (6.17)

Потери активной и реактивной мощности в звене

 ,

 .

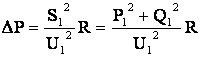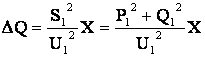Третий случай. Известны мощность в конце звена S₂ и напряжение в начале звена U₁. Требуется найти мощность в начале звена S₁ и напряжение в конце U₂. Этот случай наиболее чаще встречается в практике, так как обычно известно напряжение на шинах источника питания (электростанции, понижающей подстанции), от которого отходят линии с заданными нагрузками потребителей в конце.

Здесь невозможно, используя формулу (6.12) сразу вычислить напряжение U₂, так как неизвестна мощность в начале звена S₁. Нельзя также на основании формулы (6.10) точно определить S₁, так как для расчета потерь мощность по выражению (6.11) неизвестно напряжение в конце звена U₂. Поэтому расчет ведут  методом последовательных приближений. Исходя из величины напряжения U_1, задают начальное приближение напряжения в конце U₂=U₂⁽⁰⁾. Если нет конкретных соображений по выбору величины U₂⁽⁰⁾, ее принимают равной номинальному напряжению сети. Тогда, зная U₂⁽⁰⁾, по формулам (6.11) и (6.10) можно найти первое приближение потерь мощности в начале звена

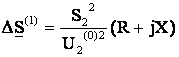                           ;                                                (6.18)

                    .                                            (6.19)

Теперь по выражению (6.12) можно найти первое приближение напряжения в конце звена

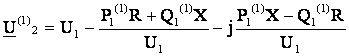       .                     (6.20)

          Подставляя в формулу (6.18) модуль напряжения , находят потери мощности в звене во втором приближении. Затем повторяют расчет по формулам (6.19) и (6.20). Расчет заканчивают, если разность между модулями напряжений  последнего и предыдущего приближений не больше заданной точности расчета.

          При этом без применения ЭВМ обычно ограничиваются расчетом первого приближения напряжения  и мощности .

          Четвертый случай. Известны мощность в начале звена  и напряжение в конце  . Требуется определить мощность в конце звена  и напряжение в начале . Как и в третьем случае, здесь используют метод последовательных приближений. Вначале, задавшись начальным приближением напряжения  по формулам (6.17) и (6.16) находят в первом приближении потери мощности  и мощность . Затем по выражению 96.5) определяют первое приближение напряжения .

          При расчете сетей с номинальным напряжением 110 кВ и ниже, полученные выше формулы (6.5) и (6.12) для определения напряжений., можно упростить. Для таких сетей характерно либо примерное равенство активного и индуктивного сопротивлений, либо некоторое повышение активного сопротивления над индуктивным. При этом передаваемая активная мощность  соизмерима с реактивной. В результате поперечная составляющая падения напряжения, определяемая по формулам (6.8) или (6.14). мала и ее влияние на модуль напряжения  или  9см.формулы (6.9) и (6.15)) незначительно.

          Если пренебречь поперечной составляющей падения напряжения, можно получить упрощенные аналогичные (6.5) и (6.12) для расчета напряжений:

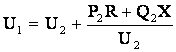                                           ;                                             (6.21)

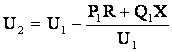                                            .                                             (6.22)

          В сетях напряжением 220 кВ и выше, в которых, как правило, >R и P>Q, величина поперечной составляющей падения напряжения значительна и пренебрегать ею нельзя.

6.4. Расчет режима линии электропередачи

          Используя зависимости, полученные в § 6.3 для разных случаев расчета звена электрической сети, рассмотрим порядок электрических расчетов линии электропередачи. Как отмечалось в § 4.2 разные линии имеют несколько различные схемы замещения. Рассмотрим расчет режима линии, которая представляется полной П-образной схемой замещения, приведенной на рис. 6.7. В ней активная проводимость заменена потерями на корону  и , а реактивная проводимость - зарядными мощностями  и . Знак «минус» перед последними означает. Что они направлены на навстречу потерям на корону.

          Рассмотрим сначала первый случай, когда по известным мощности нагрузки  и напряжению в конце  нужно найти мощность источника питания  и напряжение  в начале линии.

          По заданному напряжению  вычислим

                                         ;    .                                   (6.23)

Мощность в конце линии в соответствии с первым законом Кирхгофа

                 .                              (6.24)

По формулам (6.6) и (6.10) найдем соответственно напряжение  и мощность  в начале линии

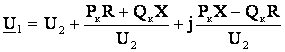                              ;                                (6.25)

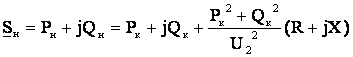                         .                   (6.26)

          По выражению (6.9) определим модуль напряжения  и по нему рассчитаем

                             ;   .                               (6.27)

Затем снова по первому закону Кирхгофа определим мощность, отдаваемую источником питания

                            .                       (6.28)

          Рассмотрим второй случай, когда задана мощность, отдаваемая источником питания , и напряжение в начале линии .

          По формулам (6.27) найдем  и  .

          По первому закону Кирхгофа поток мощности в начале линии

                                         .                                      (6.29)

          По выражению (6.12) вычислим напряжение , а по формуле (6.16) - мощность  в конце линии. Далее по формулам (6.23) найдем  и .

И, наконец, мощность нагрузки

                          .                                 (6.30)

          В третьем случае, когда задана мощность нагрузки  и напряжение в начале линии , расчет ведется по методу последовательных приближений. Зададимся начальным приближением . Найдем первое приближение

;  .

Определим мощность в конце линии

.

         Подставляя в формулу (6.26) вместо ,   и  соответственно ,  и  найдем первое приближение мощности  в начале линии. Затем по формуле (6.12) можно найти первое приближение напряжения . Если нужно добиться заданной точности определения , то описанный порядок расчета повторяем. Пусть окончательному значению  после n-ного приближения будет соответствовать какая-то мощность в начале линии . Тогда, вычислив по формулам (6.27)  и , найдем мощность источника

.

          Заметим, что при отсутствии в схеме замещения линии потерь на корону и зарядную мощность, а это имеет место в линиях низких напряжений, расчет режима линии в отношении мощности значительно упрощается. При этом и в расчете напряжений можно не учитывать поперечную составляющую падения напряжения.