![]() ;
;
![]()
![]() . (6.1)
. (6.1)
Полученную величину падения напряжения можно записать в виде
![]() .
.
Связь между напряжениями начала и конца линии в комплексной форме можно представить так
![]() . (6.2)
. (6.2)
Величину напряжения в начале линии можно найти через напряжение в конце линии и составляющие падения напряжения из треугольника ОВС
![]() . (6.3)
. (6.3)
Из второго уравнения (6.1)
видно, что при некоторых условиях (![]() ) поперечная составляющая падения
напряжения
) поперечная составляющая падения
напряжения ![]()
![]() превращается в нуль. Фактически это
имеет место, когда
превращается в нуль. Фактически это
имеет место, когда
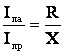 .
.
В этом случае вектора напряжений ![]() и
и ![]() совпадают по направлению и по
величине отличаются на продольную составляющую падения напряжения
совпадают по направлению и по
величине отличаются на продольную составляющую падения напряжения ![]() . Практически это встречается в линиях низких и средних
напряжений, где действительное соотношение составляющих тока
. Практически это встречается в линиях низких и средних
напряжений, где действительное соотношение составляющих тока ![]() и
и ![]() и сопротивлений линий R и X делают
и сопротивлений линий R и X делают![]() малой величиной.
малой величиной.
Отметим, что алгебраическая
разность напряжений в начале и конце линии по величине (модулю) называется
потерей напряжения. Для пояснения потери напряжения на векторной диаграмме
(рис.6.1,в) совместим поворотом относительно точки О вектор напряжения ![]() с напряжением
с напряжением ![]() . Он примет положение ОК. Разность
величин отрезков ОК и ОA и есть потеря напряжения.
Заметим, что при
. Он примет положение ОК. Разность
величин отрезков ОК и ОA и есть потеря напряжения.
Заметим, что при ![]() =0 потеря напряжения фактически равна
продольной составляющей падения напряжения.
=0 потеря напряжения фактически равна
продольной составляющей падения напряжения.
На рис. 6.1,г
несколько подробней дан фрагмент векторной диаграммы токов. Ток нагрузки ![]() , который, как отмечалось, имеет активно-индуктивный
характер, разложен на активную
, который, как отмечалось, имеет активно-индуктивный
характер, разложен на активную ![]() и реактивную
и реактивную ![]() составляющие. Аналогично в виде двух составляющих (
составляющие. Аналогично в виде двух составляющих (![]() и
и ![]() ) представлен ток в линии
) представлен ток в линии ![]() . Как видно из диаграммы, ток
. Как видно из диаграммы, ток ![]() , обусловленный активной
проводимостью линии, увеличивает активную составляющую тока нагрузки
, обусловленный активной
проводимостью линии, увеличивает активную составляющую тока нагрузки ![]() , а емкостной ток
, а емкостной ток ![]() , вызванный реактивной проводимостью
линии, уменьшает реактивную составляющую тока нагрузки
, вызванный реактивной проводимостью
линии, уменьшает реактивную составляющую тока нагрузки ![]() .
.
Аналогично построены векторные диаграммы (рис.6.2,б и 6.3,б) для линий электропередачи, схемы замещения которых соответственно приведены на рис. 6.3,а и 6.4,а. На рис.6.3 в схеме замещения отсутствует активная проводимость, что в большей степени соответствует воздушным линиям напряжением 110 и 220 кВ. Схема замещения в соответствии с рис.6.3 применяется для линий распределительных сетей напряжением 35 кВ и ниже.
Определенный интерес
представляет векторная диаграмма напряжений и токов линии, схема замещения
которой включает емкостную проводимость (рис.6.2,а), при отсутствии
нагрузки в конце линии ![]() . В этом случае по сопротивлениям
линии R и X в направлении с конца к началу протекает емкостной ток
. В этом случае по сопротивлениям
линии R и X в направлении с конца к началу протекает емкостной ток ![]() , опережающий напряжение
, опережающий напряжение ![]() на 90° (рис.6.4). По закону Ома
на 90° (рис.6.4). По закону Ома ![]() .
.
В соответствии с этим выражением на
рис.6.4 построен вектор напряжения ![]() , как видно в режиме холостого хода
напряжение в конце линии
, как видно в режиме холостого хода
напряжение в конце линии ![]() больше, чем в начале
больше, чем в начале ![]() , а при отсутствии тока нагрузки
, а при отсутствии тока нагрузки ![]() в начале линии протекает ток
в начале линии протекает ток ![]() , имеющий емкостной характер.
, имеющий емкостной характер.
6.3 Зависимости между напряжениями и мощностями
начала и конца звена электрической сети
Под звеном электрической
сети следует понимать участок ее схемы замещения, например линии
электропередачи или трансформатора (рис.6.5). так, для линии электропередачи
звеном будет участок ее П-образной схемы замещения между проводимостями
(см.рис.6.1.б). Поскольку в звене сети присутствуют только продольные
элементы схемы замещения, представленные сопротивлениями R и Х, ток в начале и конце звена
остается неизменным, равным ![]() .
.
Установим зависимости между напряжениями и мощностями начала и конца звена электрической сети для наиболее характерных для практики случаев расчета.
Первый случай.
Известны неизменные мощность и напряжение в конце звена: ![]() и
и ![]() . Требуется определить мощность
. Требуется определить мощность ![]() и напряжение
и напряжение![]() в начале звена.
в начале звена.
Здесь и далее расчет будем вести в линейных напряжениях.
Совмещая вектор напряжения ![]() с векторной осью, на основании закона Ома запишем
с векторной осью, на основании закона Ома запишем
![]()
![]() , (6.4)
, (6.4)
где ![]() - полное сопротивление.
- полное сопротивление.
Так как
![]() ,
,
то получим
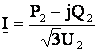 .
.
Тогда
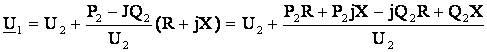 .
.
После преобразований
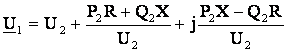 ; (6.5)
; (6.5)
![]() , (6.6)
, (6.6)
где продольная составляющая падения напряжения, вычисленная по данным конца звена, равна
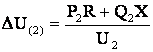 (6.7)
(6.7)
и поперечная составляющая падения напряжения
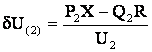 . (6.8)
. (6.8)
Модуль напряжения в начале звена
![]() . (6.9)
. (6.9)
Векторная диаграмма напряжений для этого случая показана на рис.6.6,а.
Умножив обе части
выражения (6.4) на ![]()
![]() , получим
, получим
![]()
![]()
или
![]() .
(6.10)
.
(6.10)
Таким
образом мощность в начале звена ![]() и потерь мощности в конце
и потерь мощности в конце ![]() и
потерь мощности в звене
и
потерь мощности в звене ![]() .
.
Потери мощности, найденные по данным конца звена
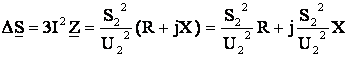 . (6.11)
. (6.11)
Потери активной и реактивной мощности в звене
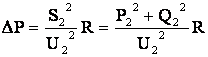 ;
;
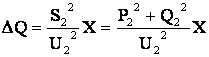 .
.
Второй
случай. Известны мощность и напряжение в начале звена: ![]() и
и ![]() .
Требуется определить мощность
.
Требуется определить мощность ![]() и напряжение
и напряжение ![]() в конце звена.
в конце звена.
Как и для первого случая по закону Ома можно записать
![]() .
.
Ток найдем по формуле
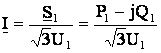 .
.
Тогда
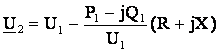 .
.
Раскрыв скобки и преобразовав, получим
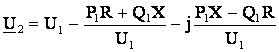 (6.12)
(6.12)
или
![]() . (6.13)
. (6.13)
Здесь продольная и поперечная составляющие падения напряжения определяются по данным начала
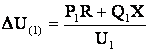 ;
; 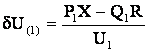 . (6.14)
. (6.14)
Величина напряжения в конце звена
![]() . (6.15)
. (6.15)
Векторная диаграмма напряжений для данного случая приведена на рис. 6.6,б.
Продольные и поперечные составляющие падения напряжения, вычисленные по данным конца звена (формулы (6.7) и (6.8)) не равны, т.е.
![]()
![]() и
и ![]() ; что
также наглядно видно из совмещенной векторной диаграммы, приведенной на рис.
6.6, в.
; что
также наглядно видно из совмещенной векторной диаграммы, приведенной на рис.
6.6, в.
![]() . (6.16)
. (6.16)
Здесь потери мощности, выраженные через параметры начала звена
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.