Проверка на прочность и выносливость двухосной тележки электровоза, страница 5

В результате рессорные комплекты каждой буксы будут иметь различные прогибы и, следовательно, различные реактивные усилия.

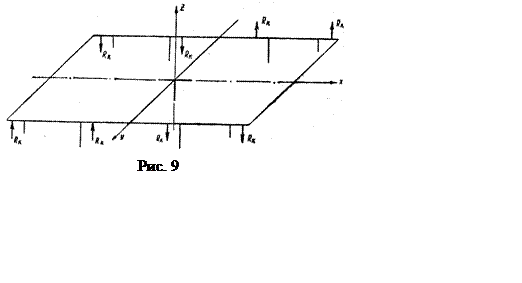
Если проанализировать распределение отдельных реакций, то окажется, что на раму действует  система вертикальных сил, попарно симметричных относительно диагоналей. Эта система называется кососимметричной нагрузкой, которая стремится повернуть боковины рамы вокруг поперечной оси в противоположные стороны (См. рис. 9).

Крутящий момент шкворневой балки в сочетании с другими силовыми факторами может вызвать опасное напряженное состояние в узлах сопряжения шкворневой балки с боковинами. В этих местах следует опасаться трещин.

Рассчитать кососимметричную составляющую можно по формуле:

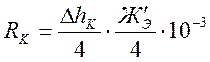
где      Δh_K – расчетная высота подъёма набегающего колеса при входе в кривую с учетом разности диаметров колес, конусообразности бандажей, неточного регулирования рессорного подвешивания, мм;

Ж’_Э – жёсткость рессорного подвешивания тележки, отнесённая к колёсной паре, кН/м.

Вычислим эквивалентную жесткость. Комплект состоит из четырёх параллельно работающих пружин с жесткостью Ж_ПР= 2200 и двух параллельно действующих листовых рессор с жесткостью Ж_Р= 1700, работающих последовательно с комплектов пружин.

Эквивалентную жесткость вычислим по формуле:

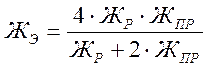
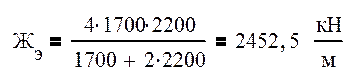
Определим величину реакции рессорных подвесок из расчета подъёма набегающего колеса при входе в кривую на Δh_K=20мм.

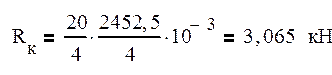
Вычислим значение изгибающего момента в опасном сечении:

М_У=3,065(0,85+2,25)=9,5, кН·м.

Напряжение в опасном сечении определяется по формуле:

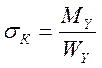
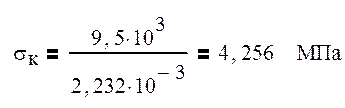
В точках 1 и 6 опасного сечения также будет происходить растяжение волокон, поэтому напряжение положительно.

11. Напряжение в опасном сечении рамы тележки от вертикальной динамической нагрузки.

Для ориентировочного расчета на прочность влияние от вертикальных колебаний при движении электровоза учитывается суммированием с напряжением от статических нагрузок максимального напряжения от динамической нагрузки. Амплитудное значение переменного напряжения получается путем умножением напряжений от статических нагрузок на коэффициент вертикальной динамики К_Д.

Коэффициент вертикальной динамики можно определить по эмпирической формуле:

;

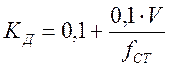где      f_СТ – статический прогиб рессорного подвешивания, мм:

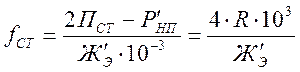
где      R – величина реакций рессорных подвесок, определенная ранее;

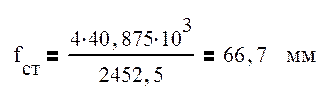
Рассчитаем значение коэффициента вертикальной динамики для разных скоростей:

Для V=0 км/ч:

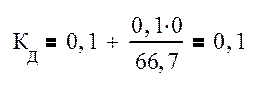
Амплитудное значение напряжения от динамической вертикальной нагрузки в МПа определяется по формуле:

;

, МПа.

где      σ_В – напряжение от статической нагрузки, вычисленное ранее.

Результаты вычислений занесём в таблицу 7.

Таблица 7.

Скорость		, МПа
V=0, км/ч;	0,1	5,588
VД=18, км/ч;	0,129	7,226
VК=100, км/ч;	0,25	13,966

12. Запас прочности в опасном сечении при наиболее неблагоприятных сочетаниях нагрузок.

После определения напряжений от основных видов нагрузки можно приступать к оценке прочности рамы по её напряженному состоянию в опасном сечении.

Для этого рассмотрим одновременное действие различных нагрузок в их возможном сочетании и проведём алгебраическое суммирование напряжение для шестой точки опасного сечения.

Расчет максимальных напряжений для различных режимов работы электровоза произведем табличным методом.

Таблица 8.

Результирующие напряжения в шестой точке опасного сечения, МПа.

Вид нагрузки	Режим работы
	Трогание	Движение в кривой с возвышением	Движение с конструкционной скоростью
Весовая	49,5	49,5	49,5
В кривой	0	73,51	0
От силы тяги	18,246	14,2	9,362
Кососимметричная	4,256	4,256	4,256
Динамическая	5,58	7,226	13,966
Сумма	77,582	148,692	77

Максимальное расчетное напряжение точка 6 опасного сечения испытывает при движении электровоза в кривой. Напряжение в точке 6 опасного сечения равно:

σ_max=148,692, МПа.

Допускаемый коэффициент запаса прочности при ориентировочном расчете определяется по формуле:

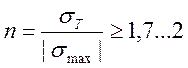
где      σ_Т=240 МПа – предел текучести стали марки Ст. 3.

|σ_Т| – абсолютное значение максимального расчетного напряжения, МПа.

n=240/148,692=1,61

Механическая прочность данной тележки обеспечена.

13. Напряжение от условий статической нагрузки.

На раму действует постоянная весовая и медленно изменяющаяся нагрузка от силы тяги, торможения и комплекса сил при движении в кривой. Кроме того, на экипаж при его движении действуют переменные силы, зависящие от верхнего строения пути, конструкции экипажа и скорости движения. Они вызывают в элементах конструкции переменные напряжения, которые в процессе длительной эксплуатации приводят к усталостным разрушениям деталей. Для таких нагрузок надо производить расчет конструкции на выносливость. Сумма напряжений от статических нагрузок в любой точке сечения представляет собой среднее напряжение σ_m циклически изменяющейся нагрузки, амплитуда которой σ_a зависит от колебаний подвижного состава.

Именно эти две величины σ_m и σ_a определяют характер переменных напряжений, действующих в различных конструкциях:

;

;

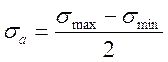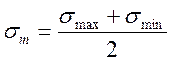Возможны два частных случая нагружения: σ_m=0 и σ_m=σ_a. Они соответствуют знакопеременному симметричному и пульсирующему циклам работы с коэффициентами асимметрии цикла:

;

;

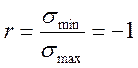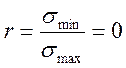Для расчета принимается среднее за время работы локомотива значение σ_m, в котором влияние медленно меняющихся нагрузок учтено весовыми коэффициентами:

где      p_КР, p_Т – отношение времени движения локомотива в кривой и в режиме тяги или торможения к общему времени движения локомотива.