Вариант 1
1) Решить уравнения, ![]()
![]()
2) Числа ![]() и
и ![]() являются
корнями уравнения
являются
корнями уравнения ![]() . Найти корни этого уравнения.
. Найти корни этого уравнения.
Вариант 2
1) Решить уравнения ![]()
![]()
2) Числа ![]() и
и ![]() являются
корнями уравнения
являются
корнями уравнения ![]() . Найти корни этого уравнения.
. Найти корни этого уравнения.
Пусть ![]() - корни
уравнения
- корни
уравнения ![]() . Составить
квадратное уравнение, корнями которого являются числа
. Составить
квадратное уравнение, корнями которого являются числа ![]()
Известно, что ![]() . Найти
. Найти ![]() .
.
Пусть ![]() - корни
уравнения
- корни
уравнения ![]() . Составить
квадратное уравнение, корнями которого являются числа
. Составить
квадратное уравнение, корнями которого являются числа ![]() .
.
Известно, что ![]() . Найти
. Найти ![]() .
.
Числа ![]() и
и ![]() являются
корнями уравнения
являются
корнями уравнения ![]() . Найти корни этого уравнения.
. Найти корни этого уравнения.
Известно, что ![]() . Найти
. Найти ![]() .
.
Пусть ![]() - корни
уравнения
- корни
уравнения ![]() . Составить
квадратное уравнение, корнями которого являются числа
. Составить
квадратное уравнение, корнями которого являются числа ![]()
Числа ![]() и
и ![]() являются
корнями уравнения
являются
корнями уравнения ![]() . Найти корни этого уравнения.
. Найти корни этого уравнения.
Известно, что ![]() . Найти
. Найти ![]() .
.
Пусть ![]() - корни
уравнения
- корни
уравнения ![]() . Составить
квадратное уравнение, корнями которого являются числа
. Составить
квадратное уравнение, корнями которого являются числа ![]()
Известно, что ![]() . Найти
. Найти ![]() .
.
Пусть ![]() - корни
уравнения
- корни
уравнения ![]() . Составить
квадратное уравнение, корнями которого являются числа
. Составить
квадратное уравнение, корнями которого являются числа ![]() .
.
Известно, что ![]() . Найти
. Найти ![]() .
.
Пусть ![]() - корни
уравнения
- корни
уравнения ![]() . Составить
квадратное уравнение, корнями которого являются числа
. Составить
квадратное уравнение, корнями которого являются числа ![]() .
.
Известно, что ![]() . Найти
. Найти ![]() .
.
1) Числа ![]() и
и ![]() являются
корнями уравнения
являются
корнями уравнения ![]() . Найти корни этого уравнения.
. Найти корни этого уравнения.
2) Решить уравнения: ![]() ,
, ![]()
1) Решить уравнения: ![]() ,
, ![]() ,
, ![]()
2) В следующем примере проверьте равносильнсть
перехода. Если переход неравеносилен, добавьте дополнительные условия так,
чтобы переход стал равносильным. ![]()
1) Решить уравнение: ![]() ,
, ![]() ,
, ![]()
2) В следующем примере проверьте равносильнсть
перехода. Если переход неравеносилен, добавьте дополнительные условия так,
чтобы переход стал равносильным ![]() .
.
1) Построить линии на координатной плоскости: ![]() ,
, ![]() ;
;
2) Найти площадь фигуры, заданной системой
неравенств 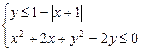
1) Построить линии на координатной плоскости ![]() ;
; ![]()
2) Найти площадь фигуры, заданной системой
неравенств 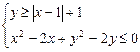
Вариант 1. 1)
При каких значениях параметра а уравнение ![]() имеет
единственное решение?
имеет
единственное решение?
2) Многочлен P(x) при делении на ![]() дает
в остатке 3, а при делении на
дает
в остатке 3, а при делении на ![]() дает
в остатке 2. Найти остаток от деления P(x) на
дает
в остатке 2. Найти остаток от деления P(x) на ![]() . 3) Решить
неравенство
. 3) Решить
неравенство ![]()
Вариант 2. 1) При
каких значениях параметра а уравнение ![]() имеет
единственное решение?
имеет
единственное решение?
2) Многочлен P(x) при делении на ![]() дает
в остатке 6, а при делении на
дает
в остатке 6, а при делении на ![]() дает
в остатке 1. Найти остаток от деления P(x) на
дает
в остатке 1. Найти остаток от деления P(x) на ![]() . 3) Решить
неравенство
. 3) Решить
неравенство ![]()
Вариант 1. 1) Построить
графики а) ![]() ; б)
; б)
![]() . 2) Для
функции
. 2) Для
функции ![]() найти
область значений; участки убывания и возрастания, написать уравнения асимптот.
3) Построить график функции
найти
область значений; участки убывания и возрастания, написать уравнения асимптот.
3) Построить график функции ![]() и
написать уравнения асимптот
и
написать уравнения асимптот
Вариант 2. 1)
Построить графики а) ![]() ;
б)
;
б) ![]() . 2) Для
функции
. 2) Для
функции ![]() найти
область значений; участки убывания и возрастания, написать уравнения асимптот.
3) Построить график функции
найти
область значений; участки убывания и возрастания, написать уравнения асимптот.
3) Построить график функции ![]() и
написать уравнения асимптот
и
написать уравнения асимптот
Контрольная (неравенства)
Вариант 1. Решить
неравенства а) ![]() ,
б)
,
б) ![]() , в)
, в) ![]()
Вариант 2. Решить
неравенства а) ![]() , б)
, б) ![]() , в)
, в)
![]()
Вариант 1. 1) Ровно в 9 часов минутная и часовая стрелки на циферблате образуют прямой угол. В какой ближайший момент времени стрелки вновь образуют прямой угол? (Найти точное время.)
Вариант 2.1) Ровно в 12 часов положения на циферблате минутной и часовой стрелок совпадают. В какой ближайший момент времени положения минутной и часовой стрелок вновь совпадут? (Найти точное время.)
1) В трапеции ABCD с основаниями AB = 5 и CD = 3 на стороне BC взята точка M так, что BM / MC = 2 / 3. Через точку M проведена прямая, параллельная основаниям трапеции. Найти отрезок этой прямой, лежащий внутри трапеции.
2) В остроугольном ![]() известны
длина медианы AM=5, медианы BN=7/2, высоты BH=3. Точка M лежит между B и H.
Найти площадь
известны
длина медианы AM=5, медианы BN=7/2, высоты BH=3. Точка M лежит между B и H.
Найти площадь![]() .
.
1) В прямоугольном треугольнике катеты равны 3 и 4. Найти радиусы вписанной и описанной окружностей.
2) В окружности радиуса 1 проведены диаметр AC
и хорда ![]() . В точке C
проведена касательная, которая пересекает продолжение AB в точке D. Найти длину
отрезков BD и CD.
. В точке C
проведена касательная, которая пересекает продолжение AB в точке D. Найти длину
отрезков BD и CD.
1) Гипотенуза прямоугольного треугольника
делится точкой касания вписанной окружности на отрезки длиной ![]() и
и ![]() . Найти
площадьтреугольника.
. Найти
площадьтреугольника.
2) Дана окружность радиуса 1. Из точки М проведены касательная МА и секущая МВ, проходящая через центр окружности. Найти расстояние от точки М до центра окружности, если МВ=2МА.
1) В трапеции ABCD с основаниями AB = 5 и CD = 3 на стороне BC взята точка M так, что BM / MC = 2 / 3. Через точку M проведена прямая, параллельная основаниям трапеции. Найти отрезок этой прямой, лежащий внутри трапеции.
2) В остроугольном ![]() известны
длина медианы AM=5, медианы BN=7/2, высоты BH=3. Точка M лежит между B и H.
Найти площадь
известны
длина медианы AM=5, медианы BN=7/2, высоты BH=3. Точка M лежит между B и H.
Найти площадь![]() .
.
1)
2) Гипотенуза прямоугольного треугольника
делится точкой касания вписанной окружности на отрезки длиной ![]() и
и ![]() . Найти
площадьтреугольника.
. Найти
площадьтреугольника.
1) В прямоугольном треугольнике катеты равны 3 и 4. Найти радиусы вписанной и описанной окружностей.
2) В окружности радиуса 1 проведены диаметр AC
и хорда ![]() . В точке C
проведена касательная, которая пересекает продолжение
. В точке C
проведена касательная, которая пересекает продолжение
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.