1.
На окружности радиуса 1 отмечены 33 точки. Доказать, что из них можно выбрать
три точки ![]() и
и
![]() так,
чтобы площадь треугольника
так,
чтобы площадь треугольника ![]() была
меньше 0,01.
была
меньше 0,01.
Решение 1. Разделим окружность на 16 замкнутых дуг длины ![]() .
Среди них найдется дуга, содержащая три отмеченные точки. Пусть
.
Среди них найдется дуга, содержащая три отмеченные точки. Пусть ![]() и
и
![]() эти
точки, расположенные в порядке следования против часовой стрелки. Так как
эти
точки, расположенные в порядке следования против часовой стрелки. Так как ![]() ,
,
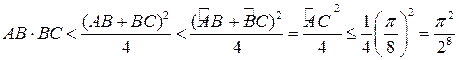 , то
, то 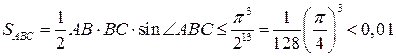 .
.
Решение 2. Как и в решении 1 получаем, что имеется три
отмеченные точки ![]() и
и
![]() ,
расположенные в порядке следования против часовой стрелки, для которых дуга
,
расположенные в порядке следования против часовой стрелки, для которых дуга ![]() .
Из всех таких треугольников
.
Из всех таких треугольников ![]() наибольшую
площадь имеет равнобедренный треугольник с основанием
наибольшую
площадь имеет равнобедренный треугольник с основанием ![]() ,
для которого дуга
,
для которого дуга ![]() .
Его площадь
.
Его площадь
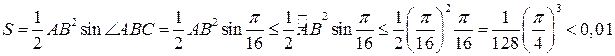 .
.
2.
Найти хотя бы одно решение матричного уравнения ![]() ,
где
,
где ![]() –
квадратная матрица 2014 порядка, на главной диагонали которой стоят нули, а вне
ее – единицы,
–
квадратная матрица 2014 порядка, на главной диагонали которой стоят нули, а вне
ее – единицы, ![]() –
нулевая матрица.
–
нулевая матрица.
Решение. Запишем уравнение в виде ![]() ,
где
,
где ![]() –
матрица 2014 порядка, все элементы которой единицы. Решение ищем в виде
–
матрица 2014 порядка, все элементы которой единицы. Решение ищем в виде ![]() ,
,
![]() .
Тогда
.
Тогда ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
В итоге мы нашли два решения
.
В итоге мы нашли два решения ![]() .
.
3. Доказать, что середины параллельных отрезков с концами на разных ветвях гиперболы образуют прямую.
Решение. Можно считать, что гипербола задана каноническим уравнением 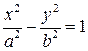 .
Для абсцисс точек пересечения прямой
.
Для абсцисс точек пересечения прямой ![]() с
гиперболой получаем квадратное уравнение
с
гиперболой получаем квадратное уравнение 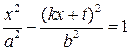 или
или
![]() .
.
Эти точки ![]() и
и
![]() существуют
и лежат на разных ветвях, если их абсциссы разных знаков, что равносильно
условию
существуют
и лежат на разных ветвях, если их абсциссы разных знаков, что равносильно
условию ![]() ;
величина
;
величина ![]() при
этом произвольна. По формуле Виета получаем абсциссу середины отрезка
при
этом произвольна. По формуле Виета получаем абсциссу середины отрезка ![]() :
:
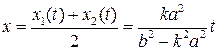 .
(1)
.
(1)
Подставляя это выражение в уравнение прямой, получаем ординату
середины отрезка ![]() :
:
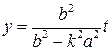 .
(2)
.
(2)
Но уравнения (1) – (2), где ![]() произвольный
параметр, являются параметрическими уравнениями некоторой прямой.
произвольный
параметр, являются параметрическими уравнениями некоторой прямой.
С вертикальными прямыми ![]() гипербола
гипербола
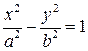 либо
не пересекается, либо пересекается в точках, лежащих на одной ветви.
либо
не пересекается, либо пересекается в точках, лежащих на одной ветви.
4.
Найти 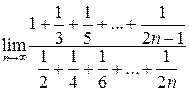 .
.
Решение 1.
Так как ряд 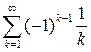 сходится,
то существует конечный
сходится,
то существует конечный 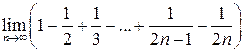 .
Так как гармонический ряд
.
Так как гармонический ряд ![]() расходится,
то
расходится,
то 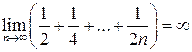 .
Поэтому
.
Поэтому
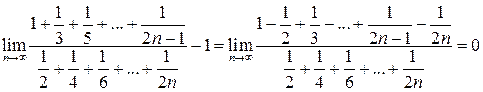 , а
, а 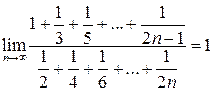 .
.
Решение 2. Так как 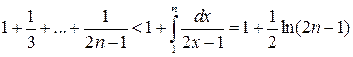 ,
,
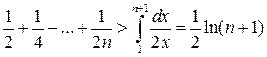 , то
, то 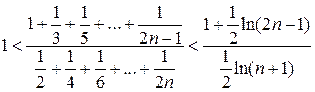 .
.
Используя правило Лопиталя, получаем 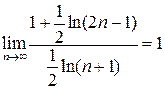 .
Поэтому
.
Поэтому 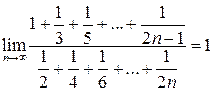 .
.
Решение 3 (не использующее рядов и интегралов). 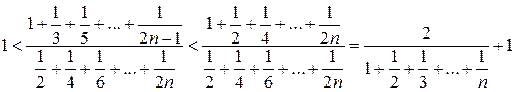 .
.
При ![]()
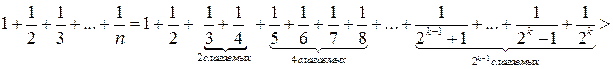
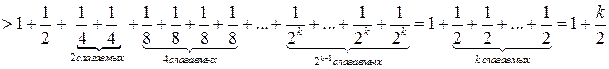 .
.
Поэтому 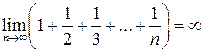 и
и
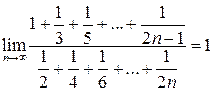 .
.
5.
Для функции 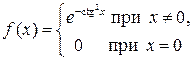 найти
найти
![]() .
.
Решение 1.
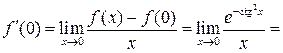
![]()
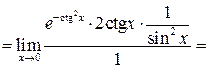
![]()
![]()
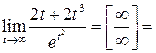
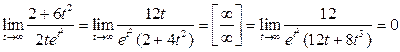 .
.
Решение 2. 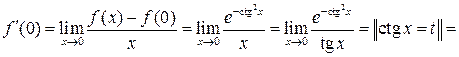
![]()
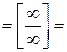
![]() .
.
Замечание. Хотя ![]() при
при
![]() ,
но, как нетрудно проверить,
,
но, как нетрудно проверить, ![]() не
эквивалентна
не
эквивалентна ![]() ,
поэтому нельзя заменять
,
поэтому нельзя заменять 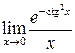 на
на
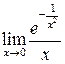 .
.
6. Пусть ![]() –
отношение многочленов,
–
отношение многочленов, ![]() .
Доказать, что график функции
.
Доказать, что график функции ![]() имеет
невертикальную асимптоту.
имеет
невертикальную асимптоту.
Решение. Пусть 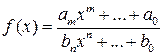 ,
где
,
где ![]() ,
,
![]() .
Покажем, что
.
Покажем, что ![]() .
Предположим противное:
.
Предположим противное: ![]() .
Так как
.
Так как 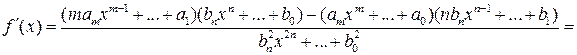
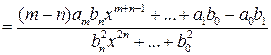 ,
,
то 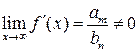 при
при
![]() и
и
![]() при
при
![]() ,
в противоречие с условием
,
в противоречие с условием ![]() .
Таким образом, на самом деле
.
Таким образом, на самом деле ![]() и
потому существует конечный
и
потому существует конечный ![]() .
Это равносильно существованию горизонтальной асимптоты.
.
Это равносильно существованию горизонтальной асимптоты.
7.
Найти промежутки монотонности и экстремумы функции 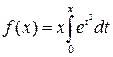 .
.
Решение 1. Функция определена на всей числовой прямой. Ее
производная 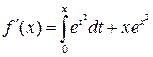 обращается
в нуль при
обращается
в нуль при ![]() .
Так как для всех
.
Так как для всех ![]()
![]() ,
то
,
то ![]() при
при
![]() ,
,
![]() при
при
![]() .
Следовательно, функция на промежутке
.
Следовательно, функция на промежутке ![]() убывает,
на промежутке
убывает,
на промежутке ![]() возрастает,
в точке
возрастает,
в точке ![]() имеет
минимум, равный 0.
имеет
минимум, равный 0.
Решение 2. Можно обойтись и без производных. При ![]()
![]() –
произведение неотрицательных возрастающих функций и потому также возрастающая
функция. При
–
произведение неотрицательных возрастающих функций и потому также возрастающая
функция. При ![]()
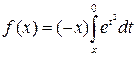 –
произведение неотрицательных убывающих функций и потому убывающая функция.
–
произведение неотрицательных убывающих функций и потому убывающая функция.
Решение 3. Возрастание ![]() на
промежутке
на
промежутке ![]() доказываем,
как и в решении 2. Так как функция четная:
доказываем,
как и в решении 2. Так как функция четная: 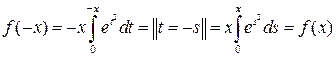 ,
из ее возрастания на
,
из ее возрастания на ![]() следует
убывание на
следует
убывание на ![]() .
.
8.
Найти все функции ![]() такие,
что для любого
такие,
что для любого ![]()
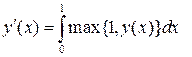 и
и
![]() .
.
Решение. Пусть ![]() –
искомая функция. Обозначим
–
искомая функция. Обозначим
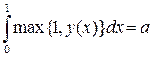 .
.
Ясно, что ![]() .
Так как
.
Так как ![]() –
постоянная, то
–
постоянная, то ![]() .
Из начального условия
.
Из начального условия ![]() находим
находим
![]() ,
,
![]() .
Подставим
.
Подставим ![]() в
уравнение. Так как
в
уравнение. Так как
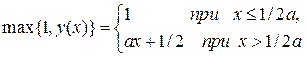 , то при
, то при ![]() получим
последовательно
получим
последовательно
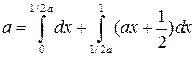 ,
,
![]() ,
,
![]() ,
,
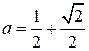 .
.
При ![]() ,
соответственно, получим
,
соответственно, получим ![]() ,
что невозможно.
,
что невозможно.
Итак, искомая функция
одна: 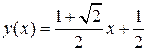 .
.
9.
Пусть функция ![]() ,
непрерывно дифференцируема, не обращается в нуль и ее производная
,
непрерывно дифференцируема, не обращается в нуль и ее производная ![]() при
при
![]() (т.е.
(т.е.
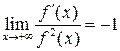 ).
Доказать, что
).
Доказать, что ![]() .
.
Решение 1. Так как 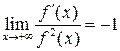 ,
то найдется такое число
,
то найдется такое число ![]() ,
что
,
что 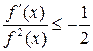 при
при
![]() .
Тогда при
.
Тогда при ![]() получаем
получаем
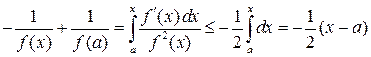 ,
,
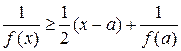 .
.
Поэтому 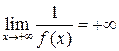 и
и
![]() .
.
Заметим также, что из того, что 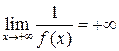 ,
а
,
а ![]() ,
следует положительность
,
следует положительность ![]() при
всех
при
всех![]() .
.
10. Сходится ли ряд 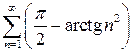 ?
?
Решение 1. Покажем, что ![]() при
при
![]() .
Действительно,
.
Действительно,
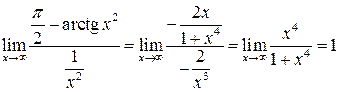 .
.
Так как ряд ![]() сходится,
то по предельному признаку сравнения сходится и заданный ряд.
сходится,
то по предельному признаку сравнения сходится и заданный ряд.
Решение 2. Обозначим ![]() .
Тогда
.
Тогда ![]() ,
,
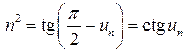 ,
,
![]() ,
,
![]() и
ряд сходится.
и
ряд сходится.
Решение 3. Так как функция ![]() ,
,
![]() положительна
и убывает, то можно применить интегральный признак сходимости.
положительна
и убывает, то можно применить интегральный признак сходимости. 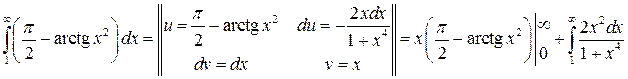
Так как 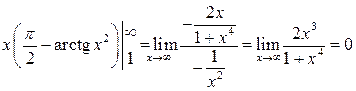 ,
,
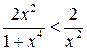 ,
а интеграл
,
а интеграл ![]() сходится,
то интеграл
сходится,
то интеграл 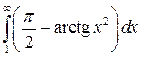 также
сходится. По интегральному признаку ряд сходится.
также
сходится. По интегральному признаку ряд сходится.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.