Определение предпоследней цифры в десятичной записи числа. Определение матрицы, обратной к квадратной матрице

РЕШЕНИЯ ЗАДАЧ ДЛЯ СТУДЕНТОВ 1 КУРСА

1.  Последняя цифра в десятичной записи числа  , , равна 4. Найти предпоследнюю цифру.

Решение. Число  оканчивается на 5, следовательно, две его последние цифры – 25. Соответственно, у числа   две последние цифры 24.

2.  На окружности радиуса 1 отмечены 2013 точек. Доказать, что на окружности существует точка, сумма расстояний от которой до отмеченных точек больше 2013.

Решение. Пусть  – отмеченные точки. Возьмем на окружности две диаметрально противоположные точки  и . Тогда

, .

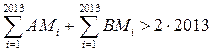Следовательно, л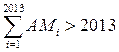ибо , либо .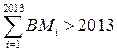

3.  Найти определитель матрицы , если   , .

Решение. У матрицы  пропорциональные строки, поэтому ее определитель равен нулю.

4.  Найти матрицу, обратную к квадратной матрице го порядка  с элементами   при  и  при .

Решение. Запишем матрицу в виде , где  – матрица, все элементы которой равны 1. Будем искать обратную матрицу в виде . Из условия  получаем . Ясно, что . Поэтому ,   и .

5.  Доказать, что для любого   .

Решение. Из неравенства , верного для всех ,  , при   получаем . Так как , то  и, окончательно,  .

6.  Решить уравнение . Здесь  – целая часть числа  – наибольшее целое число  .

Решение. При  уравнение решений не имеет, так как  и . При   , поэтому получаем уравнение   и решение .  При    и получаем уравнение   и решение .   При   получаем уравнение   и решение . Ясно, что  решением не является. При   уравнение решений не имеет, так как  и . Итак, решения уравнения: .

7.  Сколько действительных корней имеет уравнение ?

Решение. Рассмотрим функцию . Так как , то  при  и ,   при  и при ,   при . Поэтому на промежутке  наименьшее значение  равно  и  уравнение не имеет корней на этом промежутке. На промежутке    возрастает и меняет знак. Поэтому уравнение имеет единственный корень.

8.  Найти .

Решение.  Так как

.

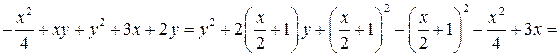
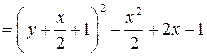
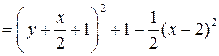то

, а   .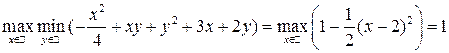

Ответ: 1.

9.  Найти .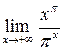

Решение. Используя  правило Лопиталя и неравенство ,  получаем  .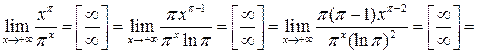

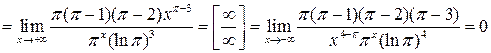Ответ: 0.

10.  Для функции  найти .

Решение. Обозначим, ,.   Тогда . При любом  имеем

, , . 

.

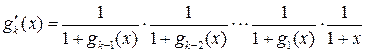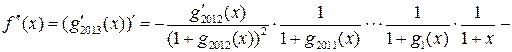
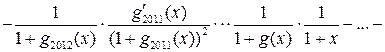
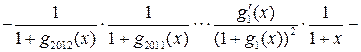
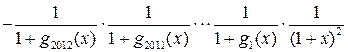В этой сумме 2013 слагаемых. При  каждое слагаемое равно -1. Следовательно,  .