Математика \ Математика

Показательная и логарифмическая функции

Страницы работы

4 страницы (Word-файл)

Посмотреть все страницы

Скачать файл

Содержание работы

Показательная и логарифмическая функции.

Показательная функция определена на всем множестве действительных чисел при любом положительном основании . Множество значений показательной функции – это множество всех положительных действительных чисел (). Для любых действительных x и y при верны следующие равенства:

1. ;

2. ;

3. ;

4. ;

5. ;

Если , то функция убывает; если , то функция возрастает.

График показательной функции приведен на рис. 1.

Упражнение 6.

Выясните, какое из чисел x, y больше, если: a) ; b) ?

Утверждение 3. Пусть . Тогда, если , то , а если , то .

Действительно, поскольку , то функция возрастает. Отсюда при имеем , а при имеем .

Упражнение 7.

Пусть . Докажите, что при и при .

Задача 1.54. Определите без калькулятора какое из чисел больше: a) или ; b) или ; c) или ?

Решение. Для a) представим числа в виде и , отсюда . Для b) заметим, что и , отсюда . Для c) сделаем такие оценки:

(1.19)

В справедливости неравенств (1.19) легко убедиться, возводя обе части каждого неравенства в квадрат. Из возрастания показательной функции с основанием, большим единицы, следует, что и . Сравним между собой числа и . Возведем оба числа в степень и сравним между собой и . Имеем: . Итак, мы выяснили, что .

Задача 1.55. Найдите все значения x, для которых верно равенство .

Подсказка.

Легко заметить, что значение удовлетворяет равенству (тройка чисел 3, 4, 5 довольно часто встречается в задачах). Вопрос в том, нет ли других значений? Запишите исходное равенство в виде и определите, монотонна или нет функция .

Решение. Равенство выполняется при . Предположим, что . Тогда из убывания показательной функции с основанием следует, что

Аналогично, при имеем:

Итак, равенство выполняется только при .

Задача 1.56. Решить уравнение .

Решение. Запишем уравнение в виде . Так же, как и в предыдущей задаче, для имеем: . Для имеем: . Только является корнем уравнения.

Логарифмическая функция определяется при любом положительном и не равном единице основании () как функция обратная к . Областью определения функции является множество всех положительных действительных чисел; областью значений – множество всех действительных чисел.

Для любых действительных x и y при верны следующие равенства:

7. ;

8. ;

9. ;

10. ;

11. ;

12. при ;

13. при (формула перехода к другому основанию);

14. ;

15. .

Если , то функция убывает; если , то функция возрастает.

График логарифмической функции приведен на рис. 1.

Тождества 7 и 8 следуют из формул (1.18), поскольку логарифмическая и показательная функции взаимно обратные.

При из тождеств 13 и 15 следует равенство

(1.20)

Замечание.

Отметим, что правые и левые части тождеств 3 – 6, взятые по отдельности, определены на разных множествах значений переменных x, y, a. Например, в левой части тождеств 3 и 4 переменные x и y могут быть и отрицательными, а в правых частях – только положительными. При четных значениях k в левой части тождества 5 переменная x может быть и отрицательной, а в правой части – только положительной. Эту особенность необходимо учитывать, применяя эти тождества для преобразования уравнений и неравенств. В соответствующих примерах на это будет обращено внимание.

Логарифм по основанию 10 называется десятичным и обозначается ; логарифм по основанию e называется натуральным обозначается .

Утверждение 4. Пусть . Тогда при функция убывает.

Справедливость этого утверждение следует из того, что функция положительная и возрастает.

Задача 1.57. Найти область определения функции .

Решение. Основание логарифма должно быть положительным и не равным единице, отсюда . Аргумент логарифма должен быть положительным, т. е. . Отметив все эти множества на числовой оси (рис. 1), находим их пересечение: .

Задача 1.58. Определите, является ли функция четной или нечетной, или не является ни четной, ни нечетной.

Решение. Функция определена на всей числовой оси, т. к. при всех x верно неравенство (докажите). Рассмотрим и заметим, что . Из тождества 11 следует, что

Таким образом, функция является нечетной.

Задача 1.59. Доказать, что при всех допустимых значениях верны следующие равенства:

a) ; b) ; c) .

Решение. Для a) применяя тождества 7, 13 и формулу (1.20), преобразуем

Для b) применяя формулу (1.20) запишем . Умножив обе части равенства на , получим . Отсюда следует

Для c) преобразуем правую часть равенства с помощью тождеств 9 – 13:

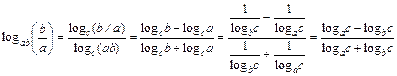Задача 1.60. Вычислить без калькулятора:

a) ; b) ; c) .

Решение. Для a) запишем и преобразуем:

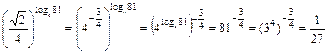Выражение b) представляет собой разность квадратов. Преобразуем его в произведение и воспользуемся тождеством 11 и формулой (1.20) :

Для c) преобразуем каждое из слагаемых:

Отсюда находим .

Задача 1.61. Упростить выражение: .

Решение. С помощью тождества 13 каждый сомножитель выразим через натуральные логарифмы; в результате получим

Задача 1.62. Выяснить без калькулятора, какое из чисел больше: или .

Решение. Каждое из этих чисел больше 1 (почему?). Чтобы разность между ними была видна лучше, вычтем из обоих чисел по и выясним, какое из чисел больше: или . Теперь оба сравниваемых числа положительны, но меньше 1 (почему?). Подберем такое разделяющее число, которое расположено на числовой оси между сравниваемыми числами. Попробуем взять в качестве разделяющего число . Убеждаемся, что , поскольку . Аналогично убеждаемся, что , поскольку (проверьте без калькулятора). Мы выяснили, что , следовательно, .