Решения задач областной олимпиады
1.
Докажите неравенство ![]() .
.
|
Решение. Разделив
обе части на |
2.
Сколько действительных решений имеет уравнение ![]() .
.
Ответ: 1 решение.
|
Решение.
Рассмотрим функцию |
3. Докажите, что функция ![]() не
является периодической.
не
является периодической.
|
Решение.
1) Покажем, что если дифференцируемая функция имеет период T, то ее
производная также имеет период T. Действительно, если f(x+T) = f(x), то |
4.
Найдите наименьшее значение функции f(x) = sin(x) на множестве ![]() .
.
Ответ: sin 1.
|
Решение:
|
5. Произведение четырех чисел — корней уравнений х2 + 2bх + с = 0 и х2 + 2сх + b = 0, где b и с — положительны, равно единице. Найдите b и с.
Ответ: b = c = 1.
Решение:
по теореме Виета ![]() Но
Но ![]() и
и ![]() т.е.
т.е. ![]() откуда b=1.
откуда b=1.
6.
Дан треугольник с вершинами A(0;
– 4), B(3, 0), C(0, 6). Найдите
расстояние вершины С до биссектрисы угла А.
Ответ: ![]() .
.
|
Решение:
|
7.
Найдите наибольший член последовательности ![]() (
(![]() .)
.)
Ответ: x2 = 6,5.
|
Решение:
|
8.
Найдите предел ![]()
Ответ: 1/11.
|
Решение:
|
9.
Найдите экстремумы функции 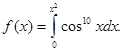 Ответ: минимум в точке x = 0 равный 0.
Ответ: минимум в точке x = 0 равный 0.
Решение:
![]() . При
. При ![]() –невозрастающая
функция на интервале
–невозрастающая
функция на интервале ![]() . При
. При ![]() – неубывающая
функция на интервале
– неубывающая
функция на интервале ![]() .
Функция имеет единственный экстремум, а именно, минимум в точке 0 и он равен
нулю.
.
Функция имеет единственный экстремум, а именно, минимум в точке 0 и он равен
нулю.
10. Верно ли, что из 100 произвольных целых чисел всегда можно выбрать: а) 15 таких, у которых разность любых двух делится на 7, б) 16 таких, у которых разность любых двух делится на 7? Ответ:a) да, б) нет.
|
Решение: Сначала заметим, что в множестве целых чисел разность любых двух делится на 7 тогда и только тогда , когда все числа этого множества имеют одинаковый остаток при делении на 7. Поэтому разделим 100 заданных чисел на 7 групп по остаткам при делении на 7. Так как групп 7, а чисел – 100 , по принципу Дирихле найдутся 15 чисел, попавших в одну группу и, следовательно, удовлетворяющих условию задачи. Значит пункт а) ответ: верно. Пункт б) ответ отрицательный. Выберем все для простоты первые 105 натуральных чисел. Разобьем их на 7 групп по остаткам при делении на 7. Тогда в каждой группе будет по 15 чисел. Выбирая 16 чисел, мы не можем всех их взять из одной группы. По принципу Дирихле найдутся два числа из разных групп. Разность этих чисел не будет делиться на 7. |
11. Найдите действительные решения системы уравнений 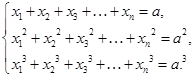 Ответ:
Ответ: ![]()
|
Решение:
1) a = 0. Из второго уравнения следует,
что x1=0, x2=0, … , xn=0.
2) |
12.
Пусть функция ![]() при всех
при всех ![]() удовлетворяет
дифференциальному уравнению
удовлетворяет
дифференциальному уравнению![]() .
Верны ли следующие утверждения:
.
Верны ли следующие утверждения:
а) если ![]() при
всех, то
при
всех, то ![]() при всех
при всех![]() ;
;
b) если ![]() при
всех, то
при
всех, то ![]() при всех
при всех![]() ?
?

Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.