РЕШЕНИЯ ЗАДАЧ ДЛЯ СТУДЕНТОВ 2–5 КУРСОВ
1. На окружности радиуса 1 отмечены 2013 точек. Доказать, что на окружности существует точка, сумма расстояний от которой до отмеченных точек больше 2013.
Решение. Пусть ![]() –
отмеченные точки. Возьмем на окружности две диаметрально противоположные точки
–
отмеченные точки. Возьмем на окружности две диаметрально противоположные точки ![]() и
и
![]() .
Тогда
.
Тогда
![]() ,
,
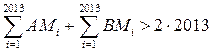 .
.
Следовательно, либо 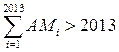 ,
либо
,
либо 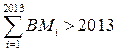 .
.
2.
Для функции ![]() найти
найти
![]() .
.
Решение 1. Обозначим![]() ,
,
![]() ,
,![]() .
Тогда
.
Тогда ![]() .
При любом
.
При любом ![]() имеем
имеем
![]() ,
,
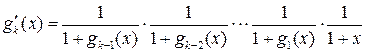 ,
,
![]() .
.
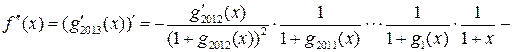
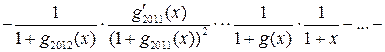
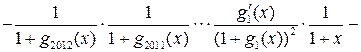
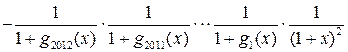 .
.
В этой сумме 2013 слагаемых. При ![]() каждое
слагаемое равно -1. Следовательно,
каждое
слагаемое равно -1. Следовательно, ![]() .
.
Решение 2. Покажем по индукции, что
![]() .
(1)
.
(1)
При ![]() это
так:
это
так: ![]() .
Пусть равенство (1) верно при
.
Пусть равенство (1) верно при ![]() .
Тогда
.
Тогда
![]()
![]()
![]() , то есть равенство (1) верно и при
, то есть равенство (1) верно и при ![]() .
По принципу математической индукции равенство верно при всех натуральных
.
По принципу математической индукции равенство верно при всех натуральных ![]() .
Так как по формуле Тейлора
.
Так как по формуле Тейлора
![]() , то
, то ![]() ,
а
,
а ![]() .
.
3.
Найти наименьшую из
площадей прямоугольных треугольников, описанных вокруг окружности радиуса ![]() .
.
Решение. Пусть ![]() и
и
![]()
![]() катеты
описанного прямоугольного треугольника. Тогда
катеты
описанного прямоугольного треугольника. Тогда ![]() ,
а гипотенуза равна
,
а гипотенуза равна ![]() .
По теореме Пифагора получаем
.
По теореме Пифагора получаем ![]() ,
,
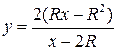 .
.
Площадь треугольника как функция
![]() :
:
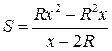 .
Так как
.
Так как 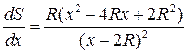 ,
то
,
то ![]() при
при
![]() и
и
![]() при
при
![]() .
Поэтому
.
Поэтому ![]()
![]() наименьшее
значение площади описанного прямоугольного треугольника.
наименьшее
значение площади описанного прямоугольного треугольника.
4.
Доказать, что функция
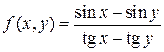 ограничена
в области
ограничена
в области ![]() .
.
Решение 1. По теореме Коши о среднем 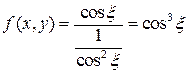 ,
где
,
где ![]() .
Следовательно, во всех точках
.
Следовательно, во всех точках ![]()
![]() .
.
Решение 2. Используя тождественные преобразования, получаем ![]() .
Так как в
.
Так как в ![]()
![]() ,
,
![]() ,
то
,
то ![]() .
.
5.
Вычислить 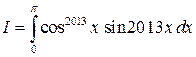 .
.
Решение 1.
![]()
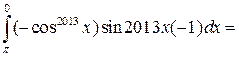
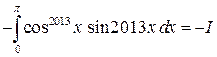 .
.
Следовательно, ![]() .
.
Решение 2. 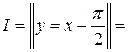
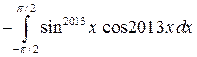 .
Получили интеграл от нечетной функции с симметричными пределами интегрирования.
Он равен нулю.
.
Получили интеграл от нечетной функции с симметричными пределами интегрирования.
Он равен нулю.
6.
Вычислить 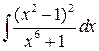 .
.
Решение. 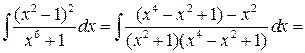
![]()
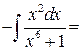
![]() .
.
7.
Вычислить
несобственный интеграл 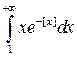 .
Здесь
.
Здесь ![]() –
целая часть числа
–
целая часть числа ![]() –
наибольшее целое число
–
наибольшее целое число ![]() .
.
Решение. Если ![]() ,
где
,
где ![]() –
натуральное число, то
–
натуральное число, то ![]() .
Поэтому
.
Поэтому
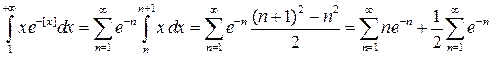 .
.
Сумма геометрического ряда 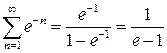 .
.
Так как для ![]()
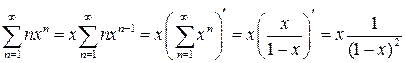 ,
то при
,
то при ![]() получим
получим
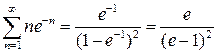 .
.
В итоге, 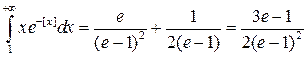 .
.
8.
Решить задачу Коши ![]() .
.
Решение. Преобразуем уравнение:
![]() ,
,
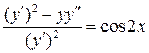 ,
,
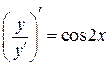 .
.
Поэтому 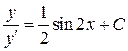 .
Из начальных условий
.
Из начальных условий ![]() .
Следовательно,
.
Следовательно,
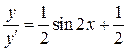 ,
,
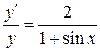 .
.
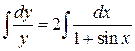 ,
,
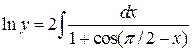 ,
,
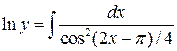 ,
,
![]() .
Из начальных условий
.
Из начальных условий ![]() .
Искомое решение имеет вид
.
Искомое решение имеет вид ![]() .
Оно определено на интервале
.
Оно определено на интервале ![]() .
.
9.
Доказать, что
дифференциальное уравнение ![]() имеет
хотя бы одно решение
имеет
хотя бы одно решение ![]() ,
стремящееся к нулю при
,
стремящееся к нулю при ![]() .
.
Решение. Характеристическое уравнение ![]() имеет
корень
имеет
корень ![]() ,
а дифференциальное уравнение – решение
,
а дифференциальное уравнение – решение ![]() ,
стремящееся к нулю при
,
стремящееся к нулю при ![]() .
.
10.
Сходится
ли ряд ![]() ,
где
,
где 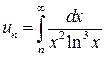 ?
?
Решение. 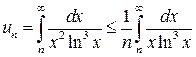
![]() .
.
Ряд 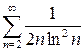 сходится
по интегральному признаку. По признаку сравнения сходится и ряд
сходится
по интегральному признаку. По признаку сравнения сходится и ряд ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.