





















Множество – совокупность отдельных, индивидуальных предметов.
Мн-ва состоят из элементов.
Мн-ва обозначаются: A, B, A1, A2
Элементы обозначаются: a, b
a Î A , принадлежит мн-ву А
Мн-во конечно, если все его элементы можно выразить конкретным числом, называемым мощностью мн-ва. ½А½- мощность мн-ва А
N- мн-во нат. чисел, бесконечное мн-во.
N = 0, 1, 2, 3, 4
![]()
![]()
![]()
![]()
![]() N = 0, 2, 4, 6
N = 0, 2, 4, 6
Мн-ва, равнозначные с N – счетные множества.
a
![]() Рациональные
числа: с= , где a,b
ÎN. Мн-во
рац. чисел счетное.
Рациональные
числа: с= , где a,b
ÎN. Мн-во
рац. чисел счетное.
b
1. Перечисление A={a, b, 5}
2. Св-ва элементов B={bi/(biÎN)&(bi>3)}
3. Индуктивный
1)0ÎN
2)если niÎN ,то ni+1Î N
4. Алгебраический
A ÈB – формула
5. Визуальный
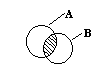
Подмножества
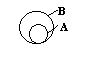
A – подмн-во B
AÎB
AÍB – содержится, но может и совпадать
Теорема. A = B тогда и только тогда, когда AÍB и BÍA
~
A - булеан
~
A={a, b, c} , A={0,{a},{b},{c},{a,b},{b,c},{a,c},{a,b,c}}
~
A=2n ,если |A| = n
~
A =Æ , A ={Æ}
1. Объединение. AÈB=C
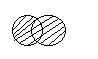
2. Пересечение. AÇ B=C
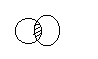
3. Сумма. A+B=C
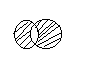
4. Разность. A\B=C
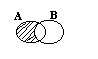
_
5.
![]() Дополнение
к мн-ву А. A=C=U \ A
Дополнение
к мн-ву А. A=C=U \ A
универсальное мн-во
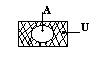 A+B
A+B
_ _ È
A+B = (AÇB)È(AÇB) / \
_ Ç Ç
A \ B = AÇB / \ / \
A _ _ B
| |
B A
1. Комутативный.
AÇ B = B Ç A
AÈ B = BÈ A
2. Ассоциативный
A Ç (B Ç C) = (A Ç B) Ç C = ABC
A È (B È C) = (A ÈB) ÈC
3. Дистрибутивный.
(AÈ B) ÇC = (A Ç C)È(B Ç C)
(AÇ B) ÇC = (A È C)Ç(B ÈC)
4. Иденпотентности (равносильности).
AÈA=A ,AÇA=A
5. Де Моргана.
___ _ _ =
AÈB= AÇB , A=A
6. Законы с пустым мн-вом.
A Ç Æ = Æ, A Ç U = A
A È A = U , A Ç A = Æ
7. Законы поглощения
AÈAB = A
(AÇU)È(AÇB)=A= AÇ(UÈB)=AÇU=A
AÇ(AÈB)=A
AAÈAB=AÈAB=A
_ _
ABÈACÈBC=ABÈAC ;
_ _ _ _ _ _
ABÈACÈUBC=ABÈACÈ(AÈA)BC=ABÈACÈABCÈABC=ABÈAC
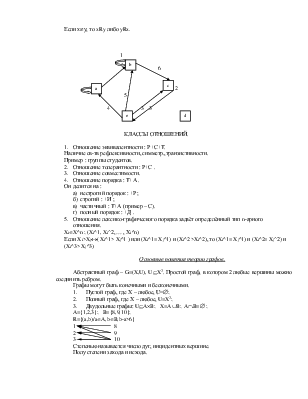
Отношения бинарные и n – арные.
1. Прямое произведение мн-в.
AxB = {(a,b)/aÎA, bÎB}
|AxB| = |A| x |B| ; (A x B) x C= A x (B x C) ; A x B¹ B x A
A x B – бинарное отношение
A x B x C – тернарное отношение
Отношение – подмножество выделенных пар.
Бинарные операции могут рассм. и на одном мн-ве A x A = A2
Отношение: RÍ A x B
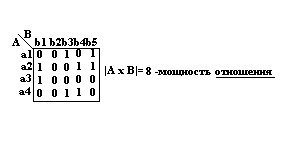
R={(a1,b1), (a2,b2), (a3,b3), (a4,b4), (a5,b5), (a6,b6), (a7,b7), (a8,b8),}
Проекция на A – область определения
Проекция на B – область значений
Элемент a1, нах. в заданном соотв. с b3,b5
Мн-ва этих значений - образ эл. a1
Сюрекция : для "а®один из В – область значений функции совпадает с В. î
Инъекция : разные а® разные b – в каждом столбце не более одной 1. ò сюрекция
Фун-я f : A®B – отображение мн-ва А в мн-во В.
Последовательности : f : N®D , где D – мн-во действительных чисел;
Функционалы : f : F®D N – мн-во натуральных чисел;
Операторы : f : F®F F – мн-во всех ф-ий действит-ых переменных.
2. Объединение
S
![]()
|
1 |
0 |
0 |
1 |
1 |
0 |
|
0 |
0 |
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
1 |
3. Композиция соответствий
RS – композиция
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]() X Y Z
X Z
X Y Z
X Z
![]()

![]()
![]()
![]()
![]()
![]()

![]()
![]() R S RS
R S RS
RS={(x,z)/ $ y:(x,y)ÎR,(y,z)ÎS}
4. Функциональное отношение.
 В
В
А
|
|
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
1 |
0 |
![]()
![]() ÚÚ Ú
ÚÚ Ú
обл. значений ф-ии
xÎA – аргумент ф-ии.
yÎB – ф-ия.
Если каждому xÎA соотв. только один yÎB, то это ФУНКЦИОНАЛЬНОЕ ОТНОШЕНИЕ.
Если разным элементам соответствуют разные значения, то инъекция.
Если отобр. Инъективно и сюръективным, то биктивное.
Если биктивное отношение рассм. на А^2, т.е. А=В, то это подстановка.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.