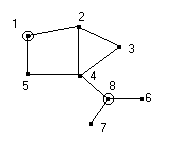
Если множество рёбер называется min, то разрез называется min. Min разрез – min число рёбер, удаляя которые мы увеличиваем число компонент связности.
{2,5,6} - min разрез; {2,4} – min разрез.
Min разрез, min число рёбер, удалением которых, мы увеличиваем число компонент связности.
Разрез должен иметь либо не иметь вообще 2 пересечения с любым базовым циклом.
Раскраска графов.
Формула Эйлера: n+f=m+2, где f – число граней.
2
В любом планарном графе существует вершина,степень вершины < 5
2m >= 3f
n+f = m+2
n+2m/3 >= m+2
3n >= m+6
но m < 3n
Конец доказательства.
Любой граф можно раскрасить 6 цветами.
Хромотическое число-min число цветов красок.
K5 нужно 5 цветов.
Связи между циклами и разрезами.
5
1 9 m-n+5=7-5+1=3
6 7
1 2 3 4 5 6 7
1 0 0 0 0 1 0
0 1 0 0 0 1 1 разрезы
0 0 1 0 1 0 1
0 0 0 1 1 0 0
0 0 1 1 1 0 0
1 1 0 0 0 1 0 циклы
0 1 1 0 0 0 1
 |
1 2 3 4 5 6 7 8
в) +1 1 0 0 1 0 0 0 v
1 1 1 1 0 0 0 0
0 1 1 1 0 0 0 0
a) +0 1 1 1 1 0 0 1 v выбираем мин число строк которые
1 0 0 1 1 0 0 0 покрывают все вершины
0 0 0 0 0 1 0 1
0 0 0 0 0 0 1 1
б) +0 0 0 1 0 1 1 1 v
-
число внутренней устойчивости графа.
Множество которое не содержит смежных вершин –устойчивое множество.
-
храматическое число графа.
Легко исследуется класс бихроматических графов( это число = 2).
Необходимым и достаточным условием бихроматичности графа является отсутствие в графе циклов нечетной длины.
Элементарный метод раскраски графа:
Эвристический метод(правила которые обычно приводят к оптимальному результату). Но он очень громозден при этом существует С в степени n вариантов раскраски где n-число вершин а С- число красок.
Будем искать всегда вершину для которой необходима новая краска.
Эту задачу можно свести к задаче о кратчайшем покрытии:
1) Отыскать все максимально пустые подграфы графа;
2) Построить матрицу бинарных отношений принадл. вершин гр.С, этим подграфам;
3) После нахождения кратчайшего покрытия этой матрицы выбираем множество вершин образующих его;
4) Получ. разбиение множества U оно и есть решение: вершина каждого класса окрашивается в свой цвет.
Делятся на два класса:
a)перечисленные задачи:
Требуется число конфигураций обладающих определенными свойствами(размещение, постановка и сочетание).
Имеется m объектов и n мест.
1. Число различных размещений U(n,m)=n в степени m;
2. Число различных перестановок. Алфавит из m символов, мы можем их упорядочить n(n-1)(n-2)…..=n! <-> P(n)=n!
3. Число различных сочетаний C(из m по n) = n(n-1)….(n-m+1)=n!/((n-m)!m!);
Выбор n предметов из общего числа предметов –m.
Для упорядоченных сочетаний C(из m по n)=n!/(n-m)!
б) оптимизационная задача: поиск конфигурации (напр. Функции стоимости обладающей определенными свойствами(экстремум))
Необходима оценка временных задач(вычислительной сложности).
Сложность задачи определяется отношением сложности исходных данных(n) и сложностью решения.
f(n)-время решения решаемой задачи с объемом исходных данных n.
F(n)=O(g(n)), если существует c такое что f(n)<=c*g(n) где g(n)-оценка сложности.
n может быть сколь угодно большим.
f(n)=O(n*n) –квадратичная сложность
f(n)=O(n) –линейная сложность
f(n)=(2в степ.n –n!)
существ. С такое что f(n)<=c*g(n)
Если g(n) – полином то имеем полиноминальную сложность.
Полиноминальный алгоритм может быть лучше чем экспоненциальный для решения практических задач с ограниченным n.
1.Метод перебора
 |
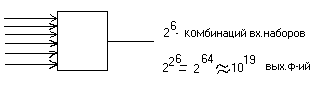А это где-то 500 лет(10 в 19-ой)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.