Основные понятия теории множеств. Способы задания множеств. Отношения бинарные и n-арные, страница 9

Задача по упаковке

Рассмотрим булеву матрицу

	операции

 

	1	2	3	4	5	6	7	8
a	1	0	1	0	0	0	1	0
ресурсы   b	0	0	0	1	1	0	0	0
c	1	1	0	0	0	0	0	0
d	0	1	0	0	0	1	0	0
e	0	0	1	1	0	0	0	1

I: 1,4,6                 Разбить столбцы на мин число                                                                                                                                                               групп, что бы каждая строка в  группе имела  не более 1 единицы.

Как разбить множество столбцов на минимальное число  групп, что бы в каждой группе каждая строка имела не более одной единицы.

I: 1,4,6

Формулы исчисления высказываний

Высказыванием называется некоторое утверждение, относительно которого можно сказать истинно оно или ложно.

Истина                Ложь

True                     False

Высказывания бывают простыми и сложными. Сложные высказывания образуются из нескольких простых посредством логических связок.

и ~ но

Для более формального исчисления высказываний вводятся следующие связки: не, и, или, или …или, если … то (импликация if ), если и, только если ( двухсторонняя iff ).

a   не a

^    и и   ^  

a     b  a или b a и b или a, или b если a, то b a iff b

^     ^        ^         ^              ^              и               и   

^    и        и        ^              и                  и              ^

и   ^      и       ^           и             ^            ^

и   и        и       и          ^              и               и        

(a или b) если (a и b)

не – ¬; – (¬a, a )

или – ⋀

и  –  ⋁

или, или – “ + “ дизъюнкция с исключением если то – “  →   “ импликация если и только если – “ ~ ” эквиваленция

1.  a, b, c – формулы(a, b, c – простые высказывания)

2.  если a и b (любые высказывания) формулы, то                

       (¬A),( A⋁B),(A⋁B),(A + B),(A→B),(A~B)

3.  других формул нет.

Упрощения:

A⋀B  = AB

(A⋁B)⋁C  ⇒ A⋁B⋁C – ассоциативная операция

(A⋁B)  ⇒ A⋁B   –  удаление конечных скобок

Приоритет операций:

1.  ¬

2.  ⋀

3.  ⋁,+

4.  →,~

Значение истинности сложного высказывания, может вычисляться как результат действий над его простыми составляющими.

(((¬a) + d)⋀(b⋁c))⋁((a→b)~(b⋀d))

(¬a + d)(b⋁c)⋁((a→b)~bd)

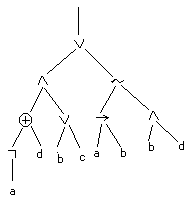
Операция перекодировки дерева

⋁ ⋀ + ¬ a d ⋁ b c ~ → a b ⋀ b d

Польская запись – LIFO last input first output

Образуем стек:

a b c d        1. d ↓⋀                       9.  b ↓ ⋀

и⋀и⋀      2. b ↓⋀                      10.   ↑ b⋁c ↓⋀

3.  ↑b⋀d↓ ⋀               11.  d ↓    ⋀

4.  b ↓  ⋀                         12.  a ↓    и

5.   a ↓ ⋀                          13.  ↑ ¬a ↓ ⋀

               6.   ↑a→b↓  ⋀              14.   ↑(¬a ) + d↓  ⋀

7. ↑(b ⋀ d)~(a→b)↓ и     15.   ↑((¬a) + d)⋀(b⋁c)↓

                    8.  c↓   и                          16.  ↑шаг↓    и

Организация стекового вычислителя.

Тавтология логики высказывания

Высказывание выполнимо, если оно может быть истинно на каком-нибудь наборе. Если высказывания истинно на всех  наборах, то они называются общезначимыми (тавтологиями). Тавтологии образуют фундамент логики высказываний. Рассмотрим основные тавтологии:

x, y, z – произвольные высказывания

1.  x →x – если существуют высказывание, то существует его значение истинности.

2.   ¬(x⋀¬x)   –  закон противоречия ( высказывание не может быть одновременно ⋁ и ⋀.

3.   x⋁¬x – закон исключенного третьего ( одно из двух, третьего не дано).