Основные понятия теории множеств. Способы задания множеств. Отношения бинарные и n-арные, страница 8

	1	2	3	4	5	6	7	8	9	10	11	12	13	14
a	0	0	0	0	0	1	1	1	0	0	0	0	1	0
b	0	1	0	0	1	0	1	0	0	0	1	0	0	0
c	1	0	0	0	0	0	0	0	1	1	0	1	0	0
d	0	0	0	1	0	0	1	0	0	0	0	0	1	0
e	0	1	0	0	1	1	0	0	0	1	0	0	0	1
f	1	0	1	0	0	0	1	0	0	1	0	1	0	0
g	0	0	0	0	1	0	1	0	0	1	1	0	0	1
h	1	0	0	1	1	1	1	1	0	0	0	0	0	0
i	0	0	1	0	0	0	0	0	1	0	0	0	0	0

Например число входов микросхем ограничено, а число выходов нужно сделать большим.

Сложность экспоненциальная.

Точный метод:

Пара a и b является совместимым, т.к. общее число аргументов не больше определенного числа.

Нужно найти кратчайшее покрытие для всех этих функций.

Функция может входить в разные подмножества, и получив ее получим точное разделение.

Приближенные методы:

1. последовательное формирование групп.

2. параллельное формирование групп.

1.  Выбираем строку с max числом аргументов, а потом добавляем к нему min число новых аргументов.

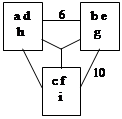
h, a, d  и т.д.

2.  Ищем таких строк, которые нельзя вместе реализовать. Поэтому их надо размножить в разных группах. И для следующих  строк смотрим, к какой группе их лучше отнести.

1   2   3   4   5  6   7   8   9 10 11 12 13 14

I

     a    0 0 0 0 0 1 1 1 0 0 0 0 1 0

d    0 0 0 1 0 0 1 0 0 0 0 0 1 0     6

h    1 0 0 1 0 1 1 1 0 0 0 0 0 0

II

     b    0 1 0 0 1 0 1 0 0 0 1 0 0 0

c     0 1 0 0 1 1 0 0 0 1 0 0 0 1     7

d     0 0 0 0 1 0 1 0 0 1 1 0 0 1

III

     e     1 0 0 0 0 0 0 0 1 1 0 1 0 0

f      1 0 1 0 0 0 1 0 0 1 0 1 0 0    6

i      0 0 1 0 0 0 0 0 1 0 0 0 0 0

f

h

С

 

A – элементы(модули)

B – эл. цепи.

 

Рассмотрим старую матрицу:

Задача: несколько элементов внутри микросхемы, но что бы по возможности , соединения были внутри микросхемы.

Эта задача комбинаторно эквивалент. предыдущей.

1

3

2

1

Минимизация ненулевых столбцов в каждой группе