4. ¬¬x~x – закон двойного отрицания.
5. x→(y→x) – истина из чего угодно.
6. ¬x→(x→y) – для любых y.
7. x(x→y)→y – “modus ponens” основное правило логического вывода в современной математике.
8. (x→y)¬y→¬x – “modus follens” основное правило доказательства от противного.
9. (x→y)(y→z)→(x→z) – закон силлогизма.
Элементы абстрактной булевой алгебры. Интерпретации.
1. Вводится понятие переменной: a, b, c …, которые могут принимать значения из множества {0,1}.
2.
Вводится 6 операций:
¬,⋁,⋀, + ,→,~,
Формы на булевом базисе называются булевыми
формами. Остальные три операции ( + ,→,~,)
выражаются через не:
a + b = ab⋁ab; a→b = a⋁b;
a~b = ab⋁ab
1. Коммутативный закон: a⋁b = b⋁a, ab = ba
2. Ассоциативный закон: (a⋁b)⋁c=a⋁(b⋁c), (ab)c=a(bc)
3. Дистрибутивный закон:
(a⋁b)c = ac⋁bc, ab⋁c=(a⋁c)(b⋁c)
4. Закон идемпотентности: aa = a, a⋁a = a
5.
Закон
Де Моргана: ¬(a⋁b) =
ab, ab = a⋁b
6. Закон двойного отрицания: ¬¬a = a
7 – 12:
a⋁1 = 1 a⋀1 = a
a⋁0 = a a⋀0 = 0
a⋁a = 1 a⋀a = 0
Отношения между формулами
Равносильные преобразования
1. A = B – равносильны
(a⋁b)c=ac⋁bc
Операция эквивалентности ~
Если A = B то A~B – тофтология
2. Формальная импликация
A ⇒ B : в любом значении, если a принимает значение 1, то и B. Обратное не всегда верно.
Говорят А – импликанта В
В – имплицента А
Операция импликации →
Если А ⇒ В, то А→В – тофтология
Так же используется понятие материальной импликации – связь между утверждениями, но это не отношение между формулами.
А – гипотеза
В – следствие
Так
же существуют отношения на основе этих отношений: ⋁
a ⋁
¬a a ¬
a
формулы в отношении и дизьюнкции.
Переход к равносильным формулам называется равносильными преобразованиями.
Рассмотрим некоторые из них.
Перейдем к расссмотрению тафтологии
А – любая формула, и если найдем такое В, что А=В, то можем рассмотреть отношение А→В
ПустьА(а,b,…,z) – тафтология, то можем получить другую тафтологию, методом подстановки вместо элемента другой формулы.
a⋁¬a a: (bc→a)
(bc→a)⋁¬(bc→a) – тафтология, принимает единицу на всех значениях
Метод подстановки – превращение одних тафтологий в другие.
Терм – любая часть формулы, которая является подфункцией, можем рассмотреть формулу как дерево, а его ветви как подформулы.
Операция равносильного преобразования над любыми формулами: в любой формуле любой терм можно заменить на равносильный ему.
ab⋁c(a⋁b) а получили ab⋁abc
ab
Если
A = B, то A ⇒B
A = B, то B ⇒A
Нормальные формы.
Рассмотрим операции √ и ∩ .
Они ассоциативны и коммутативны .
a√b√c…-можно не уточнять порядок можно написать √(a,b,c,…) также ∩(a,b,c,…)
√(a,b,c,…)=max(a,b,c,…)
∩(a,b,c,…)=min(a,b,c,…) (При этом 1>0)
Литерал — это символ или переменная , или она же под знаком отрицания .
a,b,c,…,┐a,┐b,…
ДНФ — многоместная дизъюнкция элементарных конъюнкций .
Не трудно получить ДНФ из любой формулы , в которую входят операции:
┐,√,∩,(+m2),→,~.
Сначала нужно разложить булеву формулу , оставив только ┌,√,∩,+m2:
a(+m2)b= (┐a)b√a(┐b)
a~b =(┐a) (┐b) √ab
a→b=(┐a) √b
┐(f(a,b,…)) — нужно избавиться от скобок , т.е. многократно применить правило Де Моргана и правило Шеннона.
┐F(a,┐b,…,√,∩,)=
F(a,b,…,√,∩).
Пример :
┐(((┐a)√b(┐c))d)= a((┐b)√c)√(┐d)
Дизъюнктивное разложение Шеннона :
f(a,b,c,…)=1∩f(a,b,c)=(a√(┐a))∩f(a,…)=a∩f(a,b,c,…)√(┐a)f(a,b,c)=
{a(f(a,b,…))=a(f(1,b,…))}
{(┐a)f(a,b,…)=(┐a)f(0,b,…)}
= a(f(1,b,c,…))√(┐a)f(0,b,c,…)
f=ab∩f:ab√a(┐b)∩f:a(┐b)√(┐a)b∩f:(┐a)b√(┐a)(┐b)∩f:(┐a)(┐b)
Пусть k — некоторый элемент конъюнкции
k√f =k∩(f:k)
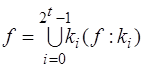
СДНФ — многоместная дизъюнкция полных элементарных конъюнкций
(полная — все ее переменные).
ДНФ можно получить из таблицы.
КНФ — многоместная конъюнкция элементарных дизъюнкций .
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.