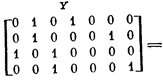
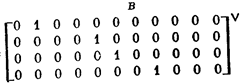

 Для примера покажем матрицу различий D,
полученную из приведенной выше матрицы X, отметив столбцы матрицы D
парами образующих их столбцов из X:
Для примера покажем матрицу различий D,
полученную из приведенной выше матрицы X, отметив столбцы матрицы D
парами образующих их столбцов из X:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.