
 Следуя сформулированным правилам, выберем в
качестве первого признака строку 1, разбивающую множество столбцов матрицы Х
на два блока:
Следуя сформулированным правилам, выберем в
качестве первого признака строку 1, разбивающую множество столбцов матрицы Х
на два блока:
 следующий выбор
падает на строку 2, и при этом множество столбцов матрицы Х разбивается
на пять блоков
следующий выбор
падает на строку 2, и при этом множество столбцов матрицы Х разбивается
на пять блоков

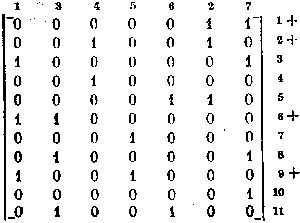
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.