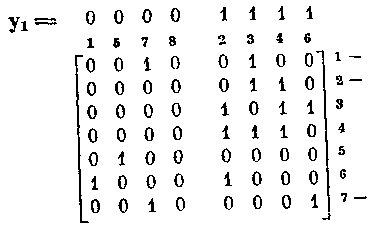 В данном случае t1 = - 01----.
Соответственно переставив столбцы, покажем порождаемое полученным вектором y1 разбиение множества столбцов матрицы X* на два равномощных блока:
В данном случае t1 = - 01----.
Соответственно переставив столбцы, покажем порождаемое полученным вектором y1 разбиение множества столбцов матрицы X* на два равномощных блока:
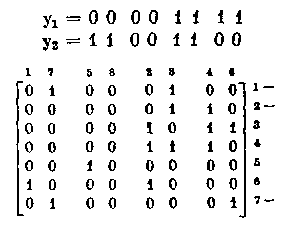
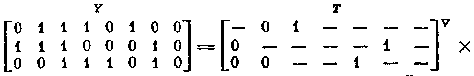
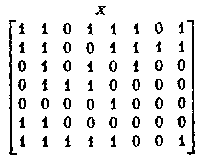 и разбиение множества столбцов становится
полным. Формируя из найденных строк матрицы У и Т, представим решение в
целом:
и разбиение множества столбцов становится
полным. Формируя из найденных строк матрицы У и Т, представим решение в
целом:
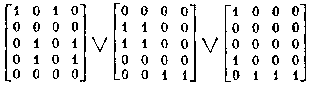
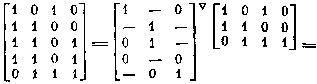 Из примера видно, что
выходная матрица У дизъюнктивно разлагается теперь уже не на единичные минеры,
а на пары единичных миноров, причем такие, что строки одного из миноров,
образующих некоторую пару, являются инверсиями строк другого минора этой же
пары. Назовем такие пары парными минорами, рассматривая далее единичные миноры,
как их частный случай, при котором задается лишь один элемент пары.
Из примера видно, что
выходная матрица У дизъюнктивно разлагается теперь уже не на единичные минеры,
а на пары единичных миноров, причем такие, что строки одного из миноров,
образующих некоторую пару, являются инверсиями строк другого минора этой же
пары. Назовем такие пары парными минорами, рассматривая далее единичные миноры,
как их частный случай, при котором задается лишь один элемент пары.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.