Математика \ Дискретная математика

Задача о кодировании. Задача о генерировании, страница 5

Точный метод. Можно предложить следующий метод нахождения точного решения этой обобщенной задачи о кратчайшем минорном покрытии булевой матрицы У: сначала найти все максимальные парные миноры (определяемые аналогично максимальным единичным ми-норам), затем построить матрицу Q бинарного отношения принадлежности единичных элементов матрицы У этим максимальным парным минорам, наконец, найти кратчайшее покрытие этой матрицы и использовать его в качестве решения поставленной задачи.

Например, входящая в рассмотренный пример матрица

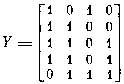
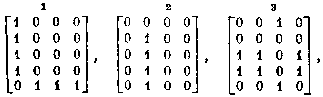
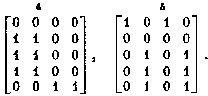обладает следующими пятью максимальными парными минорами (второй из них представляет собой вырожденный случай — максимальный единичный минор):


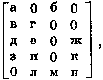Обозначив следующим образом единичные   элементы матрицы Y буквами

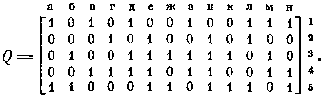построим матрицу отношения принадлежности этих элементов полученным максимальным парным минерам:

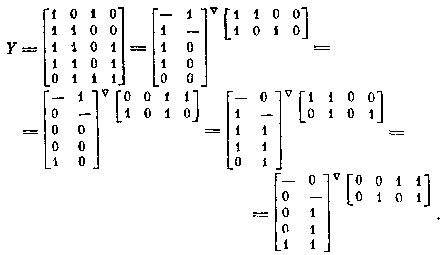
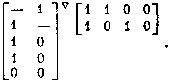Легко находится единственное кратчайшее строчное покрытие этой матрицы, включающее две последние строки. Используя его, получаем оптимальное решение для рассмотренного примера:

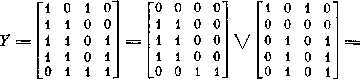
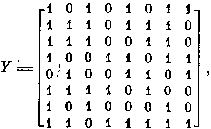Заметим, что переход от парного минора к соответствующей паре «столбец ti матрицы Т — строка хi матрицы X» неоднозначен. Дело в том, что одновременное инверсирование этих векторов не изменяет представляемого ими минора. Поэтому найденное решение порождает 2n — 1 Других, эквивалентных ему, где l — число столбцов в матрице Т.

В данном случае получаем

Приближенный    м е т о д.    Трудоемкость описанного метода зависит от размеров матрицы Q, т. е. от числа единиц в матрице Y и числа ее максимальныл парных миноров. При достаточно больших значениях этих величин метод может оказаться практически нереализуемым.

Исследуем в связи с этим возможность решения задачи о генерировании без промежуточного построения матрицы Q.

Отметим прежде всего, что различия в решении этой

задачи при двух постановках, с булевым оператором ВÚи с троичным оператором ТÑ, проявляются лишь тогда, когда в матрице Y существуют строки, находящиеся в отношении сцепляемости, определяемом следующим образом: две строки уi и yj сцепляемы, если уi V yj =1. Лишь тогда в операторной матрице Т могут существовать столбцы, содержащие как единицы, так и нули. В противном случае решение задачи генерирования для уравнения Y = ТÑХ полностью сводится к решению той же задачи для уравнения          Y = ВÚХ, с той же матрицей У.

В качестве приближенного метода решения задачи генерирования с троичной операторной матрицей Т можно рекомендовать сочетание предварительного нахождения некоторых, достаточно крупных парных миноров с последующим использованием описанного ранее метода нахождения «генератора», предложенного применительно к уравнению Y = ВÚХ и основанного на выделении в матрице У существенных и определяющих элементов. Например, рассматривая матрицу

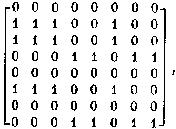выделим в ней парный минор

покрывающий довольно много единиц в матрице Y. Заменив покрытые единицы символом «—», будем беспокоиться теперь о покрытии остальных единиц, показанных в «остатке» матрицы Y:

Не находя более подходящих парных миноров, согласимся на покрытие остальных единиц максимальными единичными минерами, обратившись к, упомянутому методу его нахождения.

Обобщая отношение поглощения на троичные векторы (в данном случае строки или столбцы матрицы Y*), будем считать, что вектор а поглощает вектор Ь, если sup а ³ sup b, где оператор sup эквивалентен суперпозиции ùinfù и осуществляет отображение значений 1, —, 0 соответственно в значения 1, 1, 0. При этом те компоненты вектора а, которым соответствуют единичные значения вектора b, мажорируются последними и могут рассматриваться как несущественные.

Для полученной матрицыY*оказывается, что у2 > y3 (символ ³ используется здесь дляпоказа отношения поглощения между троичнымивекторами), у1 > у7, y2 > y7, y3 > y7, y8 > y4, y8 > y5, y1 > y3, y1 > y4, y2 > y6, y1 > y7, у6 > у8. Заменяя значения находимых несущественных

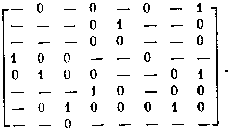элементов на «—», редуцируем матрицу Y* до

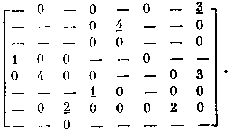Далее стандартным образом находятся определяющие элементы и определяемые ими подмножества существенных элементов. Присваивая одинаковые номера элементам, принадлежащим одному определяемому подмножеству, и подчеркивая среди них определяющий, представим результат в следующей форме:


Скачать файл