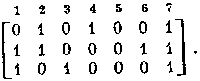
 Отображая выбранные совокупности строкиз матрицы Х
соответствующими строками операторнойматрицыВи
используя в качестве матрицы Y
полученнуюматрицу дизъюнктивного теста, мы найдемоптимальное решение данной задачи о кодировании матрицы X:
Отображая выбранные совокупности строкиз матрицы Х
соответствующими строками операторнойматрицыВи
используя в качестве матрицы Y
полученнуюматрицу дизъюнктивного теста, мы найдемоптимальное решение данной задачи о кодировании матрицы X:
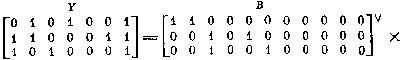

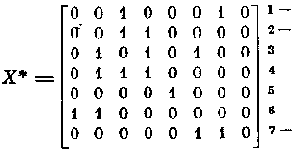
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.