Определение характеристик соединений линейных систем. Структурные преобразования линейных стационарных систем

2.3 Определение характеристик соединений

      линейных систем

2.3.1 Соединения линейных систем

Математическое описание сложной линейной системы начинается с разбиения ее на звенья направленного действия и получения описания этих звеньев в виде передаточных функций, временных (переходных) или частотных характеристик. В результате декомпозиции САУ составляется структурная схема системы, по которой затем можно получить математическое описание всей системы в целом. Если имеются уравнения всех звеньев системы, то ее описанием является система этих уравнений. Исключив из нее промежуточные переменные, можно получить одно дифференциальное уравнение высокого порядка, связывающее выходную величину системы с определенной входной величиной. Однако проще можно получить описание системы, если оперировать передаточными функциями, временными и частотными характеристиками системы. Начнем  с соединений линейных стационарных звеньев.

Рассмотрим последовательное соединение двух стационарных линейных звеньев с передаточными функциями  и  (рис.2.22).

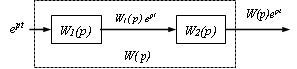Рис. 2.22 - Последовательное соединение

Если на вход последовательного соединения поступает воздействие , то его выходная величина определится соотношением  .

Следовательно, .                         (2.52)

Формула (2.52) легко обобщается на последовательное соединение любого числа стационарных линейных звеньев : если передаточные функции n соединяемых последовательно звеньев равны , . . ., , то передаточная функция соединения определяется формулой:

.                                   (2.53)

Это значит, что последовательное соединение звеньев можно заменить одним эквивалентным звеном с передаточной функцией . Так как модуль произведения комплексных чисел равен произведению модулей сомножителей, а аргумент этого произведения равен сумме аргументов сомножителей, то из (2.53) следуют формулы для амплитудной и фазовой частотных характеристик:

;                                                   (2.54)

.                                           (2.55)

Логарифмируя (2.54), получим ЛАХ последовательного соединения  звеньев:

.          (2.56)

Формулы (2.55), (2.56) показывают, что при последовательном соединении стационарных линейных звеньев их фазовые частотные характеристики и логарифмические амплитудные частотные характеристики суммируются. Из формулы (2.53) следует, что результат последовательного соединения линейных стационарных звеньев не зависит от порядка их соединения.

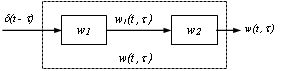Рис.2.23 - Последовательное соединение (общий случай)

Для общего случая этот результат несправедлив: из рис.2.23 следует, что весовая (импульсная переходная) функция последовательного соединения определяется следующей формулой

.

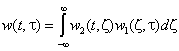При изменении порядка последовательного соединения звеньев имеем

.

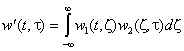Очевидно, что в общем случае . И лишь для последовательного соединения стационарных линейных звеньев справедливо следующее равенство:

.

Рассмотрим параллельное соединение двух стационарных линейных звеньев (рис.2.24).

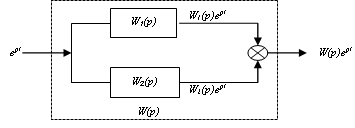Рис.2.24 - Параллельное соединение

Если на вход параллельного соединения поступает воздействие , то его выходная величина определится выражением .

Отсюда следует, что

.                                                   (2.57)

Очевидно, что эта формула также легко обобщается на любое число параллельно соединенных линейных стационарных звеньев.

Рассмотрим встречно-параллельное соединение (соединение с обратной связью) (рис.2.25).

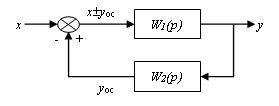
Рис.2.25 - Соединение с обратной связью

Обратная связь может быть положительной или отрицательной. Схема такого звена описывается уравнениями:

; .

Исключив из этих уравнений , получим

.

Следовательно,

.                                                 (2.58)

Итак, при любых соединениях стационарных линейных звеньев всегда получаются стационарные линейные системы, передаточные функции и частотные характеристики которых определяются при помощи элементарных алгебраических действий по передаточным функциям (частотным характеристикам) соединяемых звеньев.