Определение характеристик соединений линейных систем. Структурные преобразования линейных стационарных систем, страница 3

.

Подставляя в эту формулу выражения для  и , получим искомый результат.

 

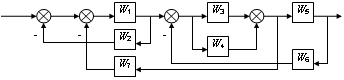
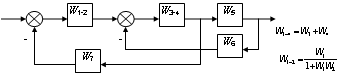
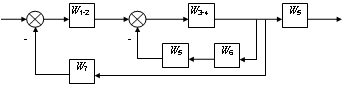
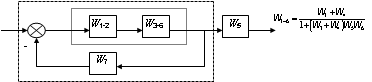
Рис.2.30 - Структурное преобразование многоконтурной схемы

2.3.3 Формула Мейсона

Второй путь получения выражения для передаточной функции сложной многоконтурной системы заключается в применении формулы Мейсона, которая дается без доказательства:

,                                       (2.59)

где - передаточные функции отдельных простых (прямых) путей от входа к выходу системы (т.е. от входного воздействия к выходной величине);

- определитель:

,                               (2.60)

где второй член равен сумме передаточных функций всех контуров; третий, четвертый и т.д. - суммы произведений двух, трех и т.д. передаточных функций контуров, не пересекающихся друг с другом (не имеющих общих вершин);

, ,  - общее число таких сочетаний;

 - определитель, полученный из  после изъятия из схемы -го прямого пути (при этом пропадают и параллельные другие пути, начинающиеся или заканчивающиеся в общих с этим путем точках), т.е. это дополнение -го пути.

Все передаточные функции в формуле (2.59) должны писаться со знаком «+» или «-» в зависимости от знаков сигналов на выходе соответствующих звеньев.

Проиллюстрируем применение формулы Мейсона на схеме, показанной на рис.2.30. Передаточные функции контуров:

; ; .

Передаточные функции прямых путей:

.

Знаменатель искомой передаточной функции согласно (2.60):

.

Соответственно,  .

Для получения искомого выражения для  остается подставить приведенные выше выражения в формулу (2.60):

.

2.3.4 Топологические преобразования

         структурных схем САУ

Передаточные функции сложных САУ можно определить по структурной схеме путем применения диаграмм прохождения сигналов (один из методов теории графов).

Подобно структурным схемам графы прохождения сигналов используются для наглядного изображения математических зависимостей в САУ. Напомним, что графом называется множество вершин и ребер. Каждому ребру соответствуют две вершины: начало и конец ребра. Вершине и ребру могут быть сопоставлены или некоторые величины, или операторы, например передаточные функции.

Основные свойства графов прохождения сигналов состоят в следующем:

*   каждая вершина, отмеченная на графе кружком или точкой, соответствует некоторой переменной рассматриваемой системы;

*   каждое ребро графа, изображаемое в виде линии со стрелкой, указывающей направление прохождения сигнала, имеет вершину-начало (входную величину) и вершину-конец (выходную величину). Если из вершины выходит несколько ребер, то все они имеют одинаковую входную величину;

*   выходная величина ребра получается как результат преобразования, осуществляемого соответствующим ребру оператором, входной величины ребра;

*   если к одной из вершин подходит несколько ребер, то величина, соответствующая этой вершине, получается алгебраическим суммированием выходных величин этих ребер.

Между структурной схемой и графом прохождения сигналов имеется прямое соответствие: прямоугольник структурной схемы соответствует ребру, а линия передачи сигнала - вершине графа.

Правила преобразования графов прохождения сигналов подобны правилам преобразования структурных схем линейных систем и приведены в табл.2.4

Таблица 2.4 - Правила преобразования сигнальных графов

Исходный граф	Эквивалентный граф

В качестве примера на рис.2.31 приведен граф прохождения сигналов, соответствующий многоконтурной структурной схеме, изображенной на рис.2.30.

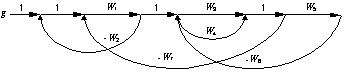
Рис.2.31 - Граф прохождения сигналов

Графы прохождения сигналов удобны для исследования сложных многоконтурных систем и особенно при использовании формулы Мейсона (2.59), так как на графах более просто прослеживаются взаимосвязи отдельных контуров.