Определение характеристик соединений линейных систем. Структурные преобразования линейных стационарных систем, страница 2

Именно поэтому метод частотных характеристик получил широкое распространение для исследования стационарных линейных систем. Вычисления по формулам (2.55), (2.56) на практике выполняются графически путем суммирования логарифмических частотных характеристик соединяемых последовательно систем.

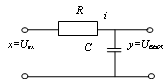
Приведем простой пример, иллюстрирующий необходимость направленности действия отдельных звеньев структурной схемы. Рассмотрим последовательное соединение двух RC-цепочек. Определим вначале передаточную функцию одной RC-цепочки (рис.2.26).

 

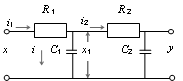
Рис. 2.26 - RC-цепочка                    Рис. 2.27 - Последовательное соединение двух RC-цепочек

Для этого достаточно применить к каждому элементу цепи законы Кирхгофа и учесть, что ток  и напряжение  на резисторе  и емкости  связаны соотношениями: ; . Справедливы следующие соотношения: ; . Следовательно, . Обозначая , получим следующее выражение для передаточной функции RC-цепочки: .

Соответствующие расчеты для последовательного соединения двух RC-цепочек (рис.2.27) приводят к следующим соотношениям:

; ; ; ; .

.

Обозначая , получим

.

Это выражение легко преобразуется к следующему виду:

,

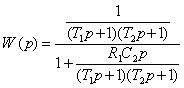т.е. вместо ожидаемого последовательного соединения (рис.2.28) получено последовательное соединение, охваченное обратной связью (рис.2.29).

 

-

 

Рис.2.28 - Последовательное соединение

 

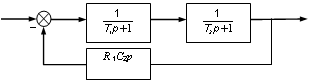Рис.2.29 - Последовательное соединение, охваченное обратной связью

Из рассмотренного примера следует, что физическое последовательное соединение двух RC-цепочек не является последовательным соединением в смысле данного выше определения.

Физическое последовательное соединение двух RC-цепочек с точки зрения ТАУ представляет собой последовательное соединение этих двух звеньев, замкнутое обратной связью, содержащей дифференцирующее звено с передаточной функцией .

Следует заметить, что не только в рассмотренном примере, но и вообще, физическое присоединение любого звена к выходу любого другого звена практически всегда будет добавлять к последовательному соединению ту или иную обратную связь. Иначе, присоединение к выходу любого звена другого звена, представляющего собой нагрузку на выходе первого звена, дает не только эффект последовательного соединения, но и дополнительный эффект обратной связи. Только при очень малой емкости  (и пропорционально большом сопротивлении , чтобы  оставалось неизменным) наш пример последовательного соединения можно рассматривать как чисто последовательное соединение без обратной связи. Т.е. для того, чтобы динамические характеристики каждого из соединяемых звеньев оставались при соединении неизменными, необходимо согласовывать входные и выходные сопротивления соединяемых звеньев. Если такое согласование оказывается практически невозможным и в нем нет практической необходимости, то следует рассматривать соединяемые звенья совместно и определять непосредственно динамические характеристики соединения.

Однако во многих случаях развязка необходима. Если это невозможно сделать согласованием сопротивлений, то применяют специальные развязывающие элементы.

2.3.2 Структурные преобразования линейных

         стационарных систем

При исследовании линейных систем важно уметь приводить их структурные схемы к форме, наиболее удобной для исследования. Так как всякая структурная схема представляет линейную систему в виде некоторых более простых линейных звеньев, точек разветвления и сумматоров, соединенных между собой различными способами, то любое преобразование структурной схемы сводится к попарной перестановке перечисленных элементов. Основное правило состоит в следующем: все входные и выходные переменные преобразуемого участка структурной схемы должны остаться неизменными. Правила преобразования сведены в табл.2.3.

Задача структурного преобразования многоконтурной схемы САУ (рис.2.30) обычно сводится к приведению исходной схемы к эквивалентной схеме с неперекрещивающимися контурами, после чего каждый из этих контуров может быть заменен эквивалентным звеном с эквивалентной передаточной функцией. Для примера на рис.2.30 передаточная функция рассматриваемой схемы равна