Устойчивость непрерывных линейных систем. Алгебраические критерии устойчивости

4 УСТОЙЧИВОСТЬ НЕПРЕРЫВНЫХ ЛИНЕЙНЫХ СИСТЕМ

4.1 Понятие об устойчивости.

      Определение устойчивости

Всякая автоматическая система должна быть прежде всего работоспособной. А это значит, что она должна нормально функционировать и быть нечувствительной к неизбежным посторонним возмущениям.

Понятие устойчивости САУ связано с ее способностью возвращаться в состояние равновесия (устойчивый режим работы) после исчезновения внешних сил, которые вывели САУ из этого состояния.

а)                                        б)                                            в)

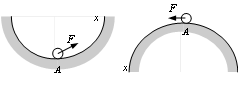
Рис. 4.1 - Состояния равновесия шара

Если подразумевать под системой некоторый шар (рис. 4.1), то можно сформулировать по отношению к нему следующее понятие об устойчивости.

1. Если шар находится на вогнутой поверхности, то при наличии силы , эквивалентной внешнему воздействию, шар можно вывести из состояния покоя (рис. 4.1, а). Предположим, что сила такова, что шар дошел до точки . Если теперь исчезает воздействие , то шар под воздействием силы тяжести после совершения нескольких колебаний около точки равновесия  придет в установившееся состояние (или состояние покоя), соответствующее точке . Это пример устойчивого равновесия (система является устойчивой).

2. Если шар находится на выпуклой поверхности и к нему приложена некоторая сила , то под воздействием этой силы шар, отклонившись в точку , после прекращения воздействия силы не придет в установившееся положение (в точку ). Такое состояние системы является неустойчивым (рис. 4.1, б).

3. Если шар находится на шероховатой ровной поверхности и к нему приложена сила , то шар выйдет из состояния равновесия и после снятия воздействия придет в новое состояние равновесия. В зависимости от величины и знака силы  шар может иметь бесчисленное множество точек равновесия. Такое состояние носит название нейтрально-устойчивого, т.е. система является нейтрально-устойчивой (рис. 4.1, в).

Таким образом, устойчивость - это свойство системы возвращаться в заданный или близкий к нему установившийся режим после всякого выхода из него в результате какого-либо воздействия.

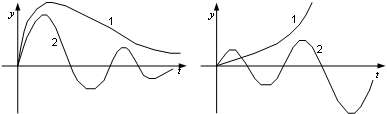
Если система неустойчива, то достаточно любого толчка, чтобы в ней начался расходящийся процесс ухода из заданного установившегося состояния. Этот процесс может быть апериодическим (кривая 1 на рис. 4.2, б) или колебательным (кривая 2 на рис. 4.2, б). В случае устойчивой системы переходный процесс, вызванный каким-либо воздействием, со временем затухает и система вновь возвращается в заданное установившееся состояние (рис. 4.2, а).

а)                                                   б)

Рис. 4.2 - Переходные процессы в САУ :

а) устойчивая САУ; б) неустойчивая САУ

Таким образом, устойчивую систему можно определить также как систему, переходные процессы в которой являются затухающими.

Это понятие устойчивости определяет устойчивость заданного установившегося режима системы. Однако система может работать в условиях непрерывно изменяющихся воздействий, когда заданный установившийся режим вообще отсутствует. С учетом условий работы можно дать следующее, более общее определение: линейная система называется устойчивой, если ее выходная переменная остается ограниченной при любых ограниченных по абсолютной величине входных возмущениях.

Поскольку для линейной системы справедлив принцип суперпозиции (1.1), то на его основании данное определение можно переформулировать следующим образом : линейная система называется устойчивой, если ее выходная переменная остается сколь угодно малой при любых достаточно малых по абсолютной величине входных возмущениях.

4.2 Условия устойчивости линейных систем

Общее необходимое и достаточное условие устойчивости линейной системы, удовлетворяющее сформулированному выше определению, состоит в следующем.

Для того, чтобы физически возможная линейная система была устойчивой, необходимо и достаточно, чтобы ее весовая (импульсная переходная) функция удовлетворяла условию:

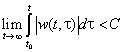,                                                            (4.1)

где  - некоторая конечная величина.

Докажем достаточность условия (4.1). Предположим, что входное возмущение представляет функцию , ограниченную по абсолютной величине: , где . Тогда

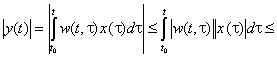
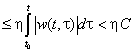.                                                         (4.2)

Таким образом, при выполнении условия (4.1) выходная переменная системы остается ограниченной при ограниченном входном возмущении. Из (4.2) следует также, что выходная переменная системы будет оставаться по абсолютной величине меньше любого заданного  при любых входных возмущениях, не превышающих по абсолютной величине .

Необходимость условия (4.1) вытекает из следующих рассуждений. Предположим, что система устойчива, но условие (4.1) для нее не выполнено, т.е.

.

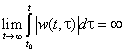Возьмем произвольную неограниченно возрастающую последовательность чисел

, .

Как следствие невыполнения условия (4.1) для любого  существует такая неограниченная последовательность моментов времени

,    при  , для которой

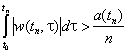,  (n = 1, 2, ...).

Рассмотрим входное возмущение вида

, ,

где                     (4.3)

- знаковая функция, тогда 

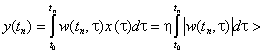
, при .

Получили противоречие и тем самым доказали необходимость условия (4.1).

Рассмотрим стационарные линейные САУ, описываемые неоднородным дифференциальным уравнением с постоянными коэффициентами вида (2.34), (2.41). Решение этого уравнения имеет вид (3.16). Нас интересует первая часть данного решения (3.21), зависящая в основном от корней характеристического уравнения (3.22). Характеристический многочлен  является знаменателем передаточной