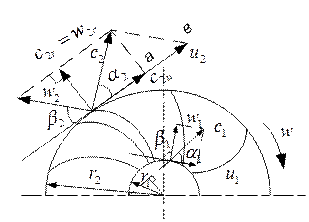
β – угол между относительной и обратным направлением окружной скорости.
Уравнение Эйлера устанавливает связь между увеличением энергии жидкости в нагнетателе и изменением ее скорости. При выводе уравнения применим некоторые допущения, которые сделаны по причине того, что кинематическая структура в криволинейных каналах чрезвычайно сложна.
Для вывода уравнения Эйлера воспользуемся уравнением моментов количества движения, согласно которому изменение момента количества движения тела равно импульсу момента внешних сил, действующих на это тело. Это уравнение применим к массе жидкости ∆т, протекающей через каналы колеса за время равное ∆t.
Моменты количества движения массы ∆т относительно оси колеса будут следующие:
 на входе:
на входе: ![]() (1)
(1)
на выходе: ![]() (2)
(2)
где r1 и r2 – соответственно радиусы движения ∆т на входе и на выходе.
![]()
![]() (3)
(3)
Считаем, что ∆L вызвано только импульсом моментов сил:
![]() (4)
(4)
где Р – момент сил, действующих на ∆т.
Учитывая уравнение (3), получим:
![]() (5)
(5)
Отношение ![]() есть
массовая производительность.
есть
массовая производительность.
![]() (6)
(6)
Домножим левые и правые части на угловую скорость:
![]() (7)
и (8)
(7)
и (8)
Произведение Рw представляет собой мощность переносимой жидкости лопастями рабочего колеса, т.е. это полезная мощность идеального или теоретического нагнетателя:
![]() (9)
(9)
С другой стороны:
![]() (10)
(10)
где НТ - теоретический напор нагнетателя.
Учитывая (9) и (10), получаем:
![]() (11)
(11)
![]() (12)
(12)
Это уравнение было получено Леонардом Эйлером в 1754г.
У многих нагнетателей среда подводится в каналы с абсолютной скоростью – с1 под прямым углом к окружной скорости – и1, в этом случае cosα1=0, тогда уравнение (12) упрощается:
![]() (13)
(13)
Справедливо для всех нагнетателей с радиальным ходом жидкости, т.е. в котором отсутствует предварительная закрутка потока.
Запишем уравнение Эйлера в другой форме: из параллелограмма скоростей с помощью теоремы косинусов можно получить:
![]() (14)
(14)
![]() (15)
(15)
Подставим (14) и (15) в (12), после преобразований получим:
![]() (16)
(16)
![]() (17)
(17)
Эта составляющая отражает изменение кинетической энергии жидкости и называется динамическим напором.
Оставшаяся часть уравнения (16) отражает выражение потенциальной энергии и представляет собой статический напор:
![]() (18)
(18)
Из уравнения (18) видно, что прирост потенциальной энергии осуществляется за счет работы центробежных сил (*) и за счет диффузорного эффекта (**), вследствие которого относительная скорость убывает.
Влияние β2 на величину теоретического напора.
Рассмотрим рабочее колесо с радиальным ходом жидкости, т.е. абсолютная скорость на входе с1 перпендикулярна окружной скорости и1. Для такого колеса справедливо упрощенное уравнение Эйлера:
![]() (1)
(1)
Из плана скоростей на выходе колеса запишем отрезок АВ:
![]() (2)
(2)
где с2и – окружная составляющая абсолютной скорости с2;
с2Г – радиальная составляющая абсолютной скорости с2;
Откуда:
![]() (3)
(3)
![]() (4)
(4)
Учитывая выражения (1), (3), (4), получим:
![]() (5)
(5)
![]() (6)
(6)
Исследуем выражение (6), т.е установим вид зависимости НТ=f(β2).
|
β2 |
0° |
90° |
180° |
|
НТ |
-∞ |
|
+∞ |
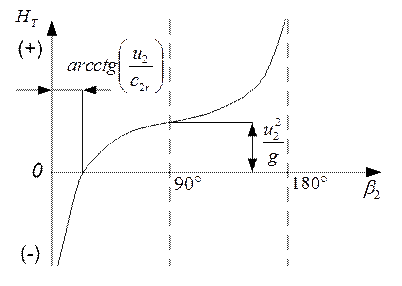
Из уравнения (5) найдем значения угла β2, при котором НТ=0:
![]()
![]() (7)
(7)
Анализ графика показывает, что НТ зависит от β2, особенно при малых (близких к нулю) и больших (близких к 180) значениях угла β2.
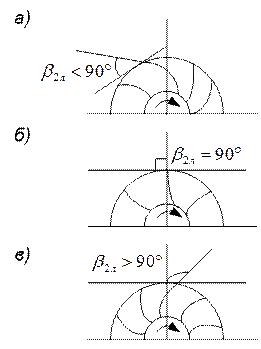 Лопастные углы. Три типа лопастей рабочего колеса.
Лопастные углы. Три типа лопастей рабочего колеса.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.