Лекция 5
Теорема 1 (Коши)
Пусть числовые ряды ![]() и
и ![]() сходятся абсолютно Þ ряд состоящий из произведений
сходятся абсолютно Þ ряд состоящий из произведений ![]() , занумерованных в произвольном
порядке будет сходится абсолютно и его сумма будет равна UV – произведение сумм начальных
рядов (из uk, vk).
, занумерованных в произвольном
порядке будет сходится абсолютно и его сумма будет равна UV – произведение сумм начальных
рядов (из uk, vk).
Доказательство
Пусть wk, k=1… –
занумерованные произведения uivj.
Пусть KÎN, nK – максимум из i и j в членах wk,k=1…K
Þ ![]()
![]() .
.
Теорема 2 (Мертенса)
Пусть ![]() и
и ![]() числовые ряды, один из которых
абсолютно сходится, а другой сходится, и U,V – их суммы Þ
числовые ряды, один из которых
абсолютно сходится, а другой сходится, и U,V – их суммы Þ ![]() , сходится и его сумма равна UV.
, сходится и его сумма равна UV.
Доказательство
Пусть ряд ![]() сходится абсолютно и Un – его частичные суммы, а ряд
сходится абсолютно и Un – его частичные суммы, а ряд ![]() сходится и Vn
– его частичные суммы.
сходится и Vn
– его частичные суммы. ![]()
![]() . Возьмем e>0 и найдем N:
. Возьмем e>0 и найдем N:
1) при ![]() .
.
2) ![]() .
.
Þ при ![]()
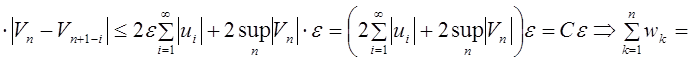
![]() .
.
Бесконечные произведения
Определение 1
Бесконечное произведение – это произведение бесконечного числа членов (такое определение некорректно).
Пусть ![]() , числовая последовательность
Þ выражение
, числовая последовательность
Þ выражение ![]() –
бесконечная числовое произведение.
–
бесконечная числовое произведение. ![]() – частичное
произведение.
– частичное
произведение.
Определение 2
Если $ конечный ненулевой
предел ![]() , то бесконечное произведение
, то бесконечное произведение ![]() сходится и P –
его величина.
сходится и P –
его величина.
Если ![]() или
или ![]() , то бесконечное произведение
расходится к 0 или к
, то бесконечное произведение
расходится к 0 или к ![]() .
.
Если ![]() не существует, то
бесконечное произведение расходится.
не существует, то
бесконечное произведение расходится.
Если бесконечное произведение сходится, то 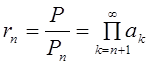 – остаток бесконечного
произведения.
– остаток бесконечного
произведения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.