Лекция 16
Следствие 1
Если h(x,y) равномерно стремится
к g(x) на X при ![]() (Y – множество
в некотором метрическом пространстве, y0 –
предельная точка Y) и Х – множество в некотором
метрическом пространстве,
(Y – множество
в некотором метрическом пространстве, y0 –
предельная точка Y) и Х – множество в некотором
метрическом пространстве, ![]() h(x,y) непрерывна в точке x0
по Х Þ g(x) непрерывна в точке x0
по Х.
h(x,y) непрерывна в точке x0
по Х Þ g(x) непрерывна в точке x0
по Х.
Доказательство
![]()
![]()
![]() .
.
Следствие 2
Если h(x,y) равномерно стремится
к g(x) на X при ![]() , Х – множество в некотором
метрическом пространстве и
, Х – множество в некотором
метрическом пространстве и ![]() h(x,y) непрерывна на Х Þ
g(x) непрерывна на Х.
h(x,y) непрерывна на Х Þ
g(x) непрерывна на Х.
Теорема 1 (о дифференцировании)
Пусть h(x,y) и ![]() определена на I´Y, где I – промежуток из R, Y – множество в некотором
метрическом пространстве, y0 – предельная
точка Y. Если
определена на I´Y, где I – промежуток из R, Y – множество в некотором
метрическом пространстве, y0 – предельная
точка Y. Если ![]() сходится равномерно на I при
сходится равномерно на I при ![]() ,
а h(x,y) сходится хотя бы в одной точке I при
,
а h(x,y) сходится хотя бы в одной точке I при ![]() Þ на "
ограниченном промежутке JÌI:
h(x,y) стремится равномерно к g(x) на J при
Þ на "
ограниченном промежутке JÌI:
h(x,y) стремится равномерно к g(x) на J при ![]() и
и ![]() стремится равномерно к g’(x) на I при
стремится равномерно к g’(x) на I при ![]() .
.
Доказательство
Возьмем произвольную последовательность ![]() Þ
для h(x,yn) и
Þ
для h(x,yn) и ![]() выполняются условия теоремы о
дифференцировании последовательности функций Þ
на " ограниченном промежутке JÌI h(x,yn)
равномерно стремится к g(x) при
выполняются условия теоремы о
дифференцировании последовательности функций Þ
на " ограниченном промежутке JÌI h(x,yn)
равномерно стремится к g(x) при ![]() на J и
на J и
![]() равномерно стремится
к g’(x) на Х при
равномерно стремится
к g’(x) на Х при ![]() .
.
Теорема 2 (об интегрируемости)
Пусть h(x,y) определенная на ![]() , Y
– множество в некотором метрическом пространстве, y0
– предельная точка Y. Если для " yÎY h(x.y) интегрируема по х на [a,b] в смысле Римана
(Мак-Шейна, Курцвейля-Хенстока) и h(x,y)
равномерно стремится к g(x) на [a,b] при
, Y
– множество в некотором метрическом пространстве, y0
– предельная точка Y. Если для " yÎY h(x.y) интегрируема по х на [a,b] в смысле Римана
(Мак-Шейна, Курцвейля-Хенстока) и h(x,y)
равномерно стремится к g(x) на [a,b] при ![]() Þ g(x)
интегрируема в том же смысле на [a,b] и
Þ g(x)
интегрируема в том же смысле на [a,b] и 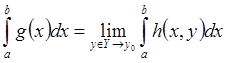 .
.
Доказательство
Возьмем произвольную последовательность ![]() Þ
для последовательности h(x,yn) выполнены
условия телоремы об интегрировании последовательности функций Þ предельная функция g(x)
интегрируема в том же смысле, что и h(x,yn)
и
Þ
для последовательности h(x,yn) выполнены
условия телоремы об интегрировании последовательности функций Þ предельная функция g(x)
интегрируема в том же смысле, что и h(x,yn)
и 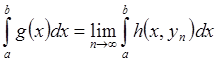 .
.
Собственные интегралы с параметром
Будем рассматривать интегралы вида 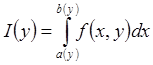 .
.
Теорема 3 (о пределе)
Пусть f(x,y) действительная (или
комплексная) функция на [A,B]´Y,
Y – множество в некотором метрическом
пространстве и y0 – предельная точка Y. Пусть f(x,y) равномерно
стремится к g(x) на [A,B]
при ![]() , а a(y) и b(y) – отображения Y в [A,B],
, а a(y) и b(y) – отображения Y в [A,B], ![]() . Для " yÎY f(x,y) интегрируема на [A,B] в одном из трех смыслов Þ g(x) тоже интегрируема на [A,B] в том же смысле и
. Для " yÎY f(x,y) интегрируема на [A,B] в одном из трех смыслов Þ g(x) тоже интегрируема на [A,B] в том же смысле и 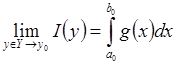 .
.
Доказательство
![]()
![]()
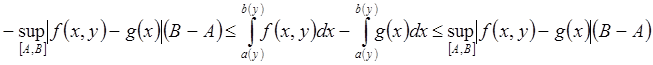
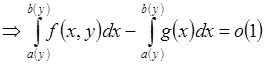 при
при ![]() .
. 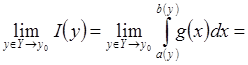
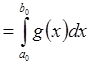 .
.
Теорема 4 (о непрерывности)
Пусть f(x,y) определена и
непрерывна на [A,B]´Y, где Y –
компакт в Rn, a(y) и b(y) непрерывные
отображения Y в [A,B] Þ 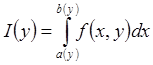 непрерывная функция на Y.
непрерывная функция на Y.
Доказательство
Для доказательства Теоремы 4 достаточно показать, что f(x,y) равномерно стремится к f(x,y0)
при ![]() на [A,B]
в " точке y0ÎY.
на [A,B]
в " точке y0ÎY.
[A,B]´Y – компакт в Rn+1, так как это ограниченное множество и оно содержит все свои предельные точки: (x0,y0) – предельная точка [A,B]´Y Þ х0 – точка соприкосновения [A,B], а y0 – точка соприкосновения Y Þ (x0,y0)Î [A,B]´Y.
Так как f(x,y)
непрерывна на компакте [A,B]´Y Þ f(x,y) равномерно
непрерывна на нем ( то есть ![]()
![]() ) Þ
) Þ ![]()
![]() Þ
есть равномерная сходимость Þ Теорема 4
следует из Теоремы 3. (Y – компакт в Rn,
так как мы пользовались теоремой о компактности в Rn).
Þ
есть равномерная сходимость Þ Теорема 4
следует из Теоремы 3. (Y – компакт в Rn,
так как мы пользовались теоремой о компактности в Rn).
Теорема 5 (о дифференцировании)
Пусть f(x,y) и ![]() непрерывны на [A,B]´[C,D]. а(y) и b(y) отображения
[C,D] в [A,B],
дифференцируемое на [C,D] Þ
непрерывны на [A,B]´[C,D]. а(y) и b(y) отображения
[C,D] в [A,B],
дифференцируемое на [C,D] Þ 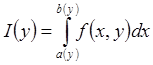 дифференцируема
на [C,D] и
дифференцируема
на [C,D] и 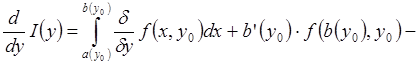
![]() .
.
Доказательство
Имеем 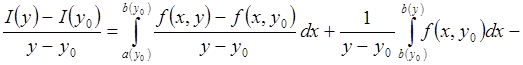
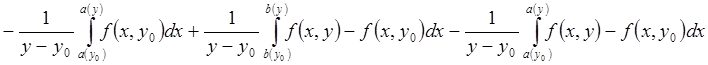
Имеем 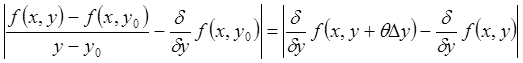 равномерно стремится
к 0 при
равномерно стремится
к 0 при ![]() на [A,B],
из-за равномерной непрерывности
на [A,B],
из-за равномерной непрерывности ![]() на
[A,B]´[C,D] и
на
[A,B]´[C,D] и ![]() Þ
Þ 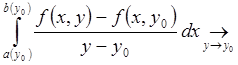
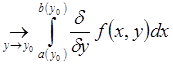 ;
;
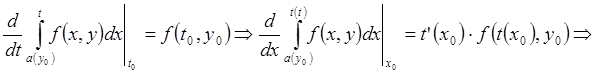
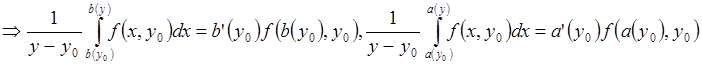
Покажем, что 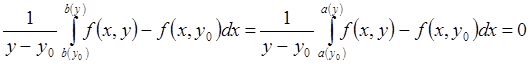
Рассмотрим 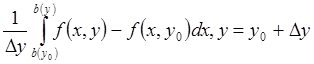 . Из-за равномерной
непрерывности f и непрерывности b(y):
. Из-за равномерной
непрерывности f и непрерывности b(y):
![]()
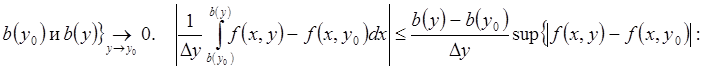 х
между b(y0)+b(y)}=O(1)o(1)=o(1) (y®y0).
х
между b(y0)+b(y)}=O(1)o(1)=o(1) (y®y0).
Теорема 6 (об интегрировании)
Пусть 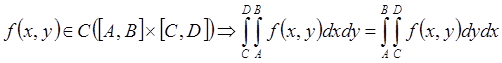 .
.
Доказательство
Имеем, что 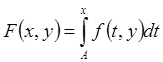 –
непрерывна на [A,B]´[C,D].
–
непрерывна на [A,B]´[C,D].
Из Теоремы 4: 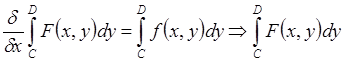 – точная
первообразная
– точная
первообразная 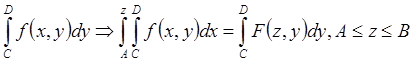 .
.
Положим z = B и получим равенство теоремы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.