Функции с параметром. Свойства равномерной сходимости. Критерий Коши равномерной сходимости

Лекция 15

Пример 1

Функция  непрерывна на R, но нигде не дифференцируема.

Доказательство

Обозначим эту функцию как  и рассмотрим  .

Имеем:

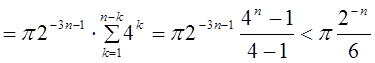. Рассмотрим

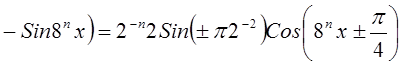. Выберем знак ± так, чтобы  попало в один из отрезков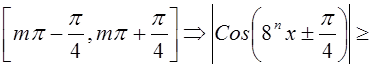   

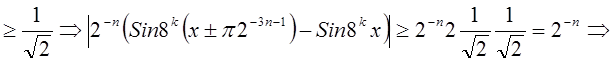
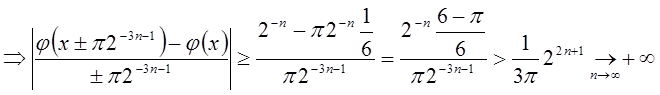
Функции с параметром

Определение 1

Пусть h(x,y) функция на  – подмножество некоторого метрического пространства и y₀ – предельная точка Y. Функция h(x,y) имеет предел в точке  при , если .

Если предел $ в " точке , то  поточечно на Е.

Функция h(x,y) при  равномерно на  стремится к функции f(x), если h(x,y) определена на  для некоторого , f(x) определена на Е и  .

Теорема 1

Функция h(x,y) равномерно стремится к f(x) на Е при  Û  равномерно стремится к f(x) на Е при .

Доказательство

1*) Докажем необходимость. Пусть выполнено условие

  .

2*) Докажем достаточность. Предположим, что h(x,y) не стремится равномерно к f(x) на Е при   . Возьмем последовательность  и найдем соответствующие  , но h(x,y) не стремится равномерно к f(x) на Е при , так как .

Свойства равномерной сходимости

1. Если h(x,y) равномерно стремится к f(x) на Е при  и  равномерно стремится к f(x) на Е’ при  ( из Теоремы 1).

2. Если h(x,y) равномерно стремится к f(x) на Е при  Þ " числа  равномерно стремится к af(x) на Е при .

Если h(x,y) равномерно стремится к f(x) на Е при  и l(x,y) равномерно стремится к g(x) на Е при  Þ  h(x,y)±l(x,y) равномерно стремится к f(x) ±g(x) на Е при .

(Следуют из свойств последовательности и Теоремы 1).

3. Если h(x,y) равномерно стремится к f(x) на Е при , а g(x) ограниченная на Е функция Þ g(x)h(x,y) равномерно стремится к g(x)f(x) на Е при .

Определение 2

Функция h(x,y) удовлетворяет условию Коши равномерной сходимости на Е при  (Y и y₀ из некоторого метрического пространства, y₀ предельная точка Y), если h(x,y) определена на  для некоторого D>0 и .

Теорема 2 (критерий Коши равномерной сходимости)

Функция h(x,y) сходится равномерно Е при  (к некоторой функции f(x)) Û h(x,y) удовлетворяет условию Коши равномерной сходимости на Е при .

Доказательство

1*) Докажем необходимость.   .

2*)Докажем достаточность. .

Теорема 3 (о перестановке пределов)

Пусть h(x,y) равномерно стремится к f(x) на Х при , Б – база в Х и  для некоторого D>0 .

Доказательство

 равномерно стремится к f(x) на Х при h®¥ и для n>N (некоторого числа, n>N ):  . Здесь мы пользовали Теоремой 1.