Числовые множества. Множества натуральных чисел. Простые числа. Некоторые классы чисел. Иррациональные числа

ЧИСЛОВЫЕ МНОЖЕСТВА

Среди числовых множеств выделяют: — множества натуральных чисел (1, 2, 3…). Они также записываются в виде 1 = 1,0000… = 1,(0). Один запятая ноль в периоде. — множества целых чисел (…, –2, –1, 0, 1, 2, …). Аналогично –1 = –1,000… = –1,(0). — множества рациональных чисел (дроби вида , где , . Любое рациональное число представляется в виде бесконечной, десятичной, периодической дроби. Любая из этих дробей — рациональное число.

Примеры: При делении на n может получиться не более n остатков. Любую дробь , можно записать в виде бесконечной, десятич-ной, периодической дроби. Доказательство: Рассмотрим знаменатель дроби n, при делении на n может получиться не больше чем n различных остатков. Примечание: Период начнется не позже, чем через n шагов деления и не будет длиннее n. Примеры обратного преобразования: 0,(3)=0,333… переведем в обычную. x = 0,333… 10х = 3,333… 9х = 3 х =

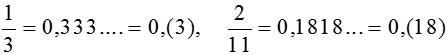
Простые числа

Подмножество N (натуральных чисел), состоящее из чисел отличных от единицы и имеющих ровно два делителя называется множеством простых чисел. Пример: 3; 7; 11… — два делителя: 1 и само число. Пусть поставлена задача выписать простые числа, одна из возможностей — решето Эратосфена. В этом методе обводится первое не зачеркнутое число, и вычеркиваются все кратные ему, дальше продолжается так же со следующим числом. Указанный способ, позволяющий выписывать первые n простых чисел, не дает ответа на вопрос конечно или бесконечно множество простых чисел.

Теорема: простых чисел бесконечно много. Доказательство: предположим противное. Пусть простых чисел конечное число и все они выписаны. 2, 3, 5, 7, …, р. Рассмотрим новое число: 2∙3∙5∙7∙…∙р + 1. При делении на все простые числа от 2 до р, в остатке будет 1, значит полученное число не делится не на одно из простых от 2 до р. Значит оно простое, либо делится на другое простое большее р число. Однако способ образования простого числа не перечисляет его подряд. Вопрос о разложении чисел на простые множители актуален и в настоящее время, в частности в криптографии.

Пример: (каждое число представляется в виде произведения степеней простых чисел — это основная теорема арифметики, такое представление единственно). Пусть А = 750, В = 3900. Найти: НОК(А, В), НОД(А, В).

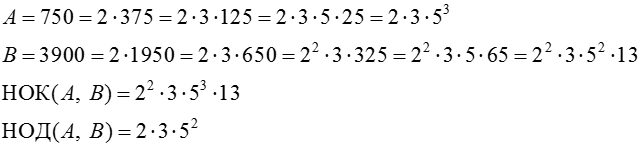
Поиск НОД и НОК разложением на простые множители в общем случае, особенно для больших чисел, достаточно сложная операция. Для нахождения НОД двух чисел древнегреческий математик Эвклид предложил алгоритм, называемый алгоритмом Эвклида. Его применение основано на следующем утверждении: если два числа имеют общий делитель, то их разность имеет то же делитель. 750 и 3900 3900 – 750∙5 = 150 750 – 150∙4 = 150 150 и 150 общий делитель 150 Если на компьютере искать все делители числа N, множество всех делителей задается от 2 до √N.

Некоторые классы чисел

Совершенные числа: совершенным называется число равное сумме всех своих делителей, за исключением самого себя. 6 = 1 + 2 + 3 28; 496; 8128; 33550336 Дружественные числа: два натуральных числа каждое из которых равно сумме правильных делителей другого (т. е. делителей, меньше этого числа). 284 и 220 1184 и 1210 17296 и 18416

Иррациональные числа

Теорема: Иррациональные числа существуют. Иррациональные числа — те, которые не могут быть записаны в виде отношения целого к натуральному; не представляются в виде периодичной, десятичной дроби. Вопрос о существовании иррациональных чисел требует доказательства. В истории математики например число π долгое время считалось частным двух натуральных чисел. Доказательство: (метод от противного). Пусть , где — несократимая дробь. Тогда , значит p2 = 2q2. Это значит, что квадрат числа p — четное число и значит само p тоже четное число. Тогда p = 2m, следует (2m)2 = 2q2, 4m2 = 2q2, 2m2 = q2, тогда q делится на 2, значит q — четное число. q = 2r. Но сократимая дробь. Противоречие.

Тем самым показано, что есть числа не представимые в виде отношения двух целых. Если иррациональные числа существуют, но не записываются в виде периодичной, десятичной дроби, они записываются в виде бесконечной, десятичной, не периодичной дроби. Все бесконечные дроби (периодичные с не периодичными вместе) образуют множество вещественных (действительных) чисел. Кстати, справедливо вложение: