ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ
Последовательность — набор из элементов любой природы, занумерованный натуральными числами. Каждый член последовательности называется ее элементом. У каждого элемента есть его номер и значение. Явная формула — соотношение между номером элемента и его значением. Пример: 1, 2, 3, 4, 5 … 3, 6, 9, 12, 15 … Рекуррентный способ — способ задания значения элемента последовательности через значение предыдущих элементов.
Задача: сколько родится кроликов за год от одной пары, если через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца после своего рождения. Ясно, что количество пар кроликов приносящих потомство в этом месяце равно сумме пар кроликов в предыдущем и предпредыдущем месяце. Обозначим число кроликов в этом месяце за an, тогда an = an–1 + an–2 Последовательность Фибоначчи: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233… Интересен факт: Это соотношение называется золотым сечением.
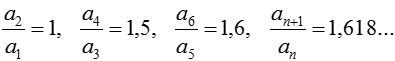
Прогрессия банковских кредитов: когда процент начисляется сразу на всю сумму займа (вместе с предыдущими процентами). Задача: В банк положили 100000 руб. под 10% годовых. Сколько будет через год, через два? Пусть b1 — начальное количество денег, q — процент. через год: b2 = b1∙q = 100000∙1,1 = 110000 p. через два: b3 = b2∙q = b1∙q2 = 110000∙1,1 = 121000 p. через 10 лет: b11 = b1∙q10 через n – 1 лет: bn = b1∙qn–1 Эта последовательность может быть предоставлена как рекуррентно, так и явно: bn = bn–1∙q bn = b1∙qn–1
Последовательность значения элементов которых представимы в таком виде называются геометрическими прогрессиями, q называется знаменателем геометрической прогрессии. Сумма конечного числа элементов прогрессии: Сумма бесконечно убывающей геометрической прогрессии: Рекуррентная формула арифметической прогрессии: an = an–1 + b d — разность арифметической прогрессии Сумма первых n элементов арифметической прогрессии:
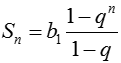
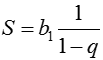
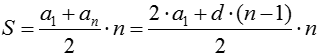
Последовательность an является бесконечно малой величиной, если для любого ε найдется номер N0 такой, что для всех N > N0 выполнено: |an| < ε. Последовательность — бесконечно малая. Число А называется пределом последовательности an, если последовательность |А – an| — бесконечно малая величина. Для последовательности пределом является 0. Пределы последовательности an: Рассмотрим последовательность: Не всякая последовательность имеет предел.
![]()
![]()
![]()
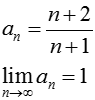
Ряды
Сумму последовательности an принято обозначать: В случае бесконечно убывающей геометрической прогрессии сумма всегда конечна. Чтобы найти сумму ряда, строят последовательность из частичных сумм ряда: Если предел последовательности SN существует, то ряд называется сходящимся. Если предела частичных сумм не существует ряд называется расходящимся.
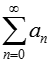
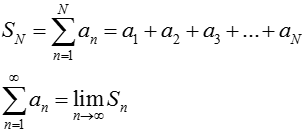
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.