Лекция 25
Теорема 1 (Вейерштрасса)
1) Для " комплекснозначной
непрерывной функции f на [a,b] и "e>0 $ многочлен P(x) (действительный,
если f действительна): ![]() .
.
2) Для " комплекснозначной
m раз непрерывно дифференцируемой (в
действительном смысле) функции f на [a,b] "e>0 $ многочлен
P(x) (действительный, если f действительна): ![]() .
.
Доказательство
При линейных преобразованиях аргумента утверждение сохраняется Þ если мы докажем утверждение для отрезка [0,1], то оно будет верно и для " отрезка (заменой ![]() отрезок [a,b] сводится
к [0,1]).
отрезок [a,b] сводится
к [0,1]).
1*) Вычитая из f(x) линейную функцию g(x)=f(0)+x(f(1)-f(0)) сведем всё к функции, обращающейся в 0 в концах отрезка – точказ 0 и 1.
2*) Вычитая из f(x) некоторый многочлен можно добиться, что их разность вместе с производными до порядка m включительно будет обращаться в 0 в концах отрезка – точках 0 и 1.
Итак, пусть h(x) непрерывная на [0,1] (непрерывная с производными h(k)(х),
k =0…m на
[0,1]), h(0) = h(1)=0 (h(k)(0)=h(k)(1)=0, k=0…m). Продолжим h
нулем на R\[0,1], это непрерывная на R
(с h(k)(x), k=0…m) функция. Пусть Kn(x) – единица из примера 4) Лекции 24: ![]() равномерно стремится на R при n®¥ к h(x) (
равномерно стремится на R при n®¥ к h(x) (![]() равномерно
стремится на R при n®¥ к h(k)(x),
k=0…m).
равномерно
стремится на R при n®¥ к h(k)(x),
k=0…m). 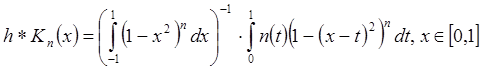 – многочлен от х.
– многочлен от х.
Определение 1
Система функций ![]() или
система
или
система ![]() – тригонометрическая система.
– тригонометрическая система. ![]() .
.
Определение 2
Тригонометрический многочлен – это конечная линейная комбинация
функций тригонометрической системы, то есть выражение вида ![]()
![]() .
.
Теорема 2 (Вейерштрасса)
1) Для " 2p-периодической комплекснозначной непрерывной
функции f и "e>0 $ тригонометрический
многочлен T(x) ( с действительными
коэффициентами an и bn, если f
действительна): ![]()
![]() .
.
2) Для " 2p-периодической комплекснозначной m раз непрерывно дифференцируемой (в смысле действительных
коэффициентов) функции f и "e>0 $ тригонометрический
многочлен T(x) (действительный, то есть с
действительными an и bn, если f действительна):
![]() .
.
Доказательство
Возьмем Kn(x) из примера 5) Лекции
24. Имеем, что ![]() равномерно
стремится к f(x) на R при n®¥ (
равномерно
стремится к f(x) на R при n®¥ (![]() равномерно стремится к f(k)(x) на R при n®¥).
равномерно стремится к f(k)(x) на R при n®¥). 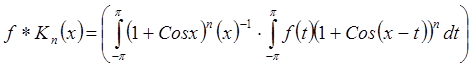 –
тригонометрический многочлен (из Теоремы 1).
–
тригонометрический многочлен (из Теоремы 1).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.