Лекция 14
Теорема 1
Пусть степенной ряд ![]() имеет
радиус сходимости R>0 Þ ряд
имеет
радиус сходимости R>0 Þ ряд ![]() , полученный почленным
дифференцированием начального ряда, имеет также радиус сходимости R и в круге сходимости есть (комплексные) производные начального
ряда.
, полученный почленным
дифференцированием начального ряда, имеет также радиус сходимости R и в круге сходимости есть (комплексные) производные начального
ряда.
Доказательство
1*) ![]() .
.
2*) Пусть ![]() . Пусть
. Пусть ![]()
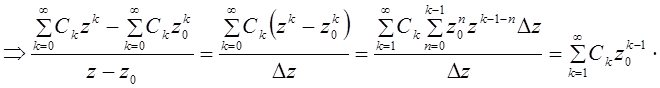
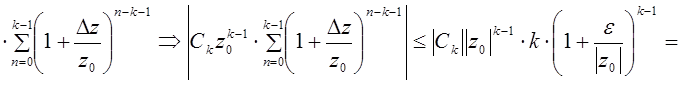
![]() –
ряд из последовательности членов сходится. По признаку Вейерштрасса ряд
–
ряд из последовательности членов сходится. По признаку Вейерштрасса ряд 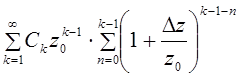 сходится равномерно при
сходится равномерно при 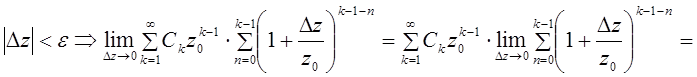
![]() .
.
Следствие 1
Степенной ряд бесконечно дифференцируем в круге сходимости (в комплексном смысле).
Следствие 2
Степенной ряд имеет (комплексную) первообразную в круге сходимости.
Теорема 2
Пусть степенной ряд ![]() имеет
радиус сходимости R>0, j(t) – непрерывное
отображение отрезка [a,b] в круг
сходимости, g(t) – непрерывная функция на [a,b] Þ
имеет
радиус сходимости R>0, j(t) – непрерывное
отображение отрезка [a,b] в круг
сходимости, g(t) – непрерывная функция на [a,b] Þ ![]() .
.
Теорема 3
Степенной ряд ![]() с радиусом
сходимости R>0 есть ряд Тейлора своей суммы.
с радиусом
сходимости R>0 есть ряд Тейлора своей суммы.
Доказательство
![]() в круге сходимости
в круге сходимости 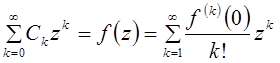 , то есть надо доказать, что
, то есть надо доказать, что 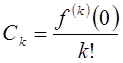 . Имеем
. Имеем 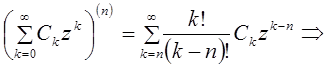 в точке z=0
имеем
в точке z=0
имеем ![]() .
.
Теорема 4 (единственность)
Пусть степенные ряды ![]() и
и ![]() с положительными радиусами
сходимости совпадают в точках
с положительными радиусами
сходимости совпадают в точках ![]() Þ эти ряды совпадают
тождественно (то есть ak=bk для
"k).
Þ эти ряды совпадают
тождественно (то есть ak=bk для
"k).
Доказательство
Из непрерывности суммы степенного ряда (в круге сходимости) следует, что в точке 0 оба ряда принимают одинаковые значения, то есть a0=b0.
Предположим, что ak=bk для k=0,1…n. Докажем, что an+1=bn+1.
Степенные ряды ![]() и
и
![]() совпадают в точках
совпадают в точках ![]() Þ степенные ряды
Þ степенные ряды ![]() и
и
![]() совпадают в точках
совпадают в точках ![]() , у них совпадают по
доказанному коэффициенты при k=0, то есть an+1=bn+1.
, у них совпадают по
доказанному коэффициенты при k=0, то есть an+1=bn+1.
Теорема 5 (Абеля)
Пусть степенной ряд ![]() сходится в
точке z0 Þ он сходится
равномерно на отрезке
сходится в
точке z0 Þ он сходится
равномерно на отрезке ![]() Þ есть непрерывные
функции на нем.
Þ есть непрерывные
функции на нем.
Доказательство
Ряд ![]() сходится равномерно
при
сходится равномерно
при ![]() по признаку Абеля.
по признаку Абеля.
Пример 1
1) Рассмотрим ![]()
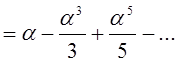 сходится при
сходится при ![]() .
.
2) Рассмотрим ![]()
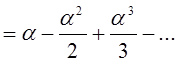 сходится при
сходится при ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.