Лекция 31
Определение 1
Ряд ![]() , или
, или ![]() – тригонометрический ряд, если
– тригонометрический ряд, если
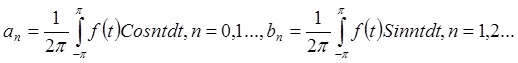 , или
, или 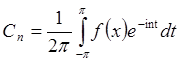 – тригонометрический ряд есть
ряд Фурье по тригонометрической системе (обозначается как
– тригонометрический ряд есть
ряд Фурье по тригонометрической системе (обозначается как ![]() ).
).
Свойства тригонометрических рядов Фурье (для 2p-периодической f, интегрируемой по Мак-Шейну)
1) (Линейность) ![]() .
.
2) (Инвариантность относительно сдвига) Если ![]()
![]() .
.
Доказательство
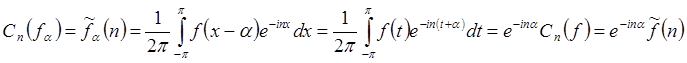
![]() .
.
3) (Инвариантность относительно симметрии) Если ![]() 2p-периодическая функция Þ
2p-периодическая функция Þ ![]() .
.
4) (Инвариантность относительно дифференцирования) Если f 2p-периодическая
всюду дифференцируемая функция и f'
интегрируемая по Мак-Шейну Þ ![]() , где
, где ![]() – почленно
продифференцированный ряд Фурье
– почленно
продифференцированный ряд Фурье ![]() .
.
Доказательство
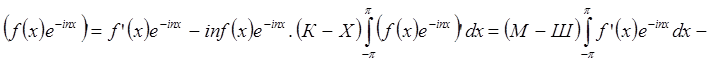
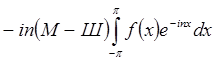 . Имеем, что
. Имеем, что 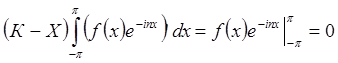 , а также
, а также 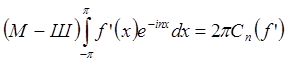 ,
, 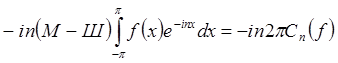 Þ
Þ ![]() .
.
5) (Коэффициенты Фурье свертки)
Если 2p-периодические ![]()
Þ ряд Фурье от ![]() .
.
Доказательство
Если ![]() Þ ряд Фурье от
Þ ряд Фурье от 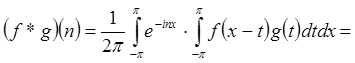 (из
теоремы о собственном интеграле)
(из
теоремы о собственном интеграле) 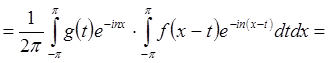
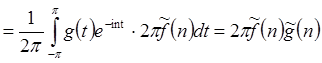 .
.
Имеем, что " функцию
интегрируемую по Мак-Шейну можно приблизить непрерывными функциями. Пусть ![]() и
и ![]() по
норме в L2[-p,p].
по
норме в L2[-p,p]. ![]() (так как
(так как ![]()
![]() )
и
)
и ![]() . Покажем, что
ряд Фурье от
. Покажем, что
ряд Фурье от ![]() к ряду Фурье от
к ряду Фурье от ![]()
![]() .
Заметим, что
.
Заметим, что 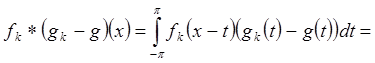
![]()
![]() и
и
![]() . Значит, ряд Фурье от
. Значит, ряд Фурье от ![]() к ряду Фурье от
к ряду Фурье от ![]() Þ
Þ
![]() .
.
6) (Равенство Парсеваля-Ляпунова) Если ![]()
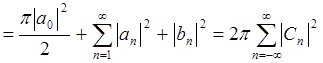 .
.
7) Если 2p-периодическая
функция ![]()
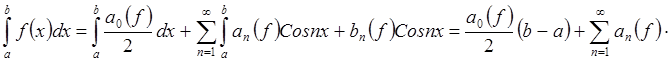
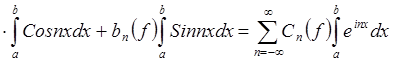 .
.
Доказательство
Для отрезка с длиной 2p –
очевидно. Рассмотрим случай, когда отрезок меньше 2p. Пусть b-a<2p Þ 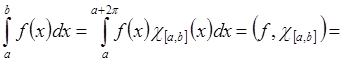
![]() ,
где c – 2p-периодическое продолжение c[a,b] .
Рассмотрим
,
где c – 2p-периодическое продолжение c[a,b] .
Рассмотрим 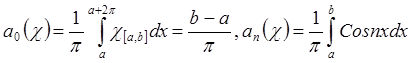
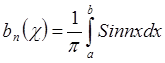 .
.
Теорема 1
Если 2p-периодическая
f интегрируемая по Мак-Шейну (на [-p,p]) Þ ![]() .
.
Доказательство
Возьмем "e>0 и найдем m: 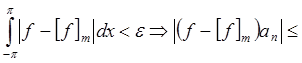
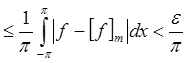 .
Аналогично
.
Аналогично ![]() .
. ![]()
![]()
![]() . Аналогично
. Аналогично ![]() .
.
8) Если f интегрируема по
Мак-Шейну Þ ![]() (то есть
(то есть ![]() , если m
не делится на k и
, если m
не делится на k и ![]() ,
если m делится на k).
,
если m делится на k).
Доказательство
1*) Если m не делится на k:
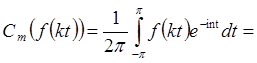
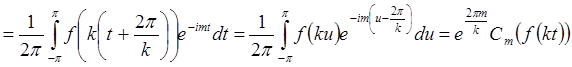 ,
так как
,
так как ![]() не кратно 2p Þ
не кратно 2p Þ ![]() .
.
2*) Если m делится на k:
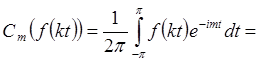
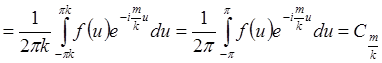 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.