Лекция 11
Свойства равномерной сходимости
Теорема 1 (о перестановке пределов)
Пусть функциональная последовательность ![]() сходится равномерно на М, Б –
база множеств в М и
сходится равномерно на М, Б –
база множеств в М и ![]() для предельной
функции
для предельной
функции ![]() .
.
Доказательство
Для выполнение теоремы необходимо и
достаточно, чтобы ![]()
![]() . Из-за равномерной сходимости
на М имеем:
. Из-за равномерной сходимости
на М имеем: ![]() .
.
Следствие 1
Пусть функциональная последовательность ![]() сходится равномерно на Е к f(x), где ЕÌМ –
метрическое пространство, а – предельная точка Е и
сходится равномерно на Е к f(x), где ЕÌМ –
метрическое пространство, а – предельная точка Е и ![]() .
.
Следствие 2
Пусть функциональная последовательность ![]() сходится равномерно на Е
к f(x), где ЕÌМ – метрическое пространство, fk(x)
непрерывны на Е Þ
f(x) непрерывна на Е.
сходится равномерно на Е
к f(x), где ЕÌМ – метрическое пространство, fk(x)
непрерывны на Е Þ
f(x) непрерывна на Е.
Следствие 3
Пусть К – компакт в метрическом пространстве М, С(К) – множество
непрерывных на К функций с нормой ![]() – банахово
пространство, сходимость в котором эквивалентна равномерной сходимости на К.
– банахово
пространство, сходимость в котором эквивалентна равномерной сходимости на К.
Доказательство
Легко проверить свойства нормы. ![]() по
норме Û
по
норме Û ![]() ,
так как
,
так как ![]() . Докажем, что нормированное
пространство полное, то есть " последовательность
Коши сходится, то есть пусть fk –
последовательность Коши в С(К) Þ
. Докажем, что нормированное
пространство полное, то есть " последовательность
Коши сходится, то есть пусть fk –
последовательность Коши в С(К) Þ ![]()
![]() , то есть выполнен критерий
Коши равномерной сходимости на К Þ fk равномерно сходится к f(x)ÎС(К), то есть
, то есть выполнен критерий
Коши равномерной сходимости на К Þ fk равномерно сходится к f(x)ÎС(К), то есть ![]() С(К) по норме в С(К).
С(К) по норме в С(К).
Теорема 2
Пусть функциональный ряд ![]() сходится
равномерно на М, Б – база в М, и для
сходится
равномерно на М, Б – база в М, и для ![]() .
.
Следствие 4
Пусть ![]() сходится равномерно
на ЕÌМ – метрическое
пространство, а – предельная точка Е и
сходится равномерно
на ЕÌМ – метрическое
пространство, а – предельная точка Е и ![]()
![]() .
.
Следствие 5
Если ![]() сходится равномерно
на ЕÌМ – метрическое
пространство, и все uk(x) непрерывны
на Е Þ
сходится равномерно
на ЕÌМ – метрическое
пространство, и все uk(x) непрерывны
на Е Þ ![]() непрерывен на Е.
непрерывен на Е.
Теорема 3
Пусть дана функциональная последовательность ![]() на промежутке IÌR,
на промежутке IÌR, ![]() сходится равномерно
на I, fk(х)
сходятся в некоторой точке
сходится равномерно
на I, fk(х)
сходятся в некоторой точке ![]() сходятся
равномерно на " ограниченном
промежутке JÌI к f(x),
f(x) дифференцируема на I
и
сходятся
равномерно на " ограниченном
промежутке JÌI к f(x),
f(x) дифференцируема на I
и ![]() .
.
Доказательство
1*) Докажем, что fk(х)
сходятся равномерно на ограниченном промежутке JÌI. ![]()
![]()
![]()
![]()
![]() Þ выполнен
критерий равномерной сходимости на J Þ fk(х)
равномерно сходятся на " ограниченном
промежутке J.
Þ выполнен
критерий равномерной сходимости на J Þ fk(х)
равномерно сходятся на " ограниченном
промежутке J.
2*) Пусть х0 – некоторая
точка I, рассмотрим ![]()
для ![]() . Функциональная
последовательность
. Функциональная
последовательность ![]() сходится равномерно
при
сходится равномерно
при ![]()
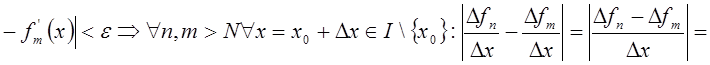
![]() .
. ![]() .
По Следствию 1 получаем, что
.
По Следствию 1 получаем, что ![]() .
.
Теорема 4
Пусть дан функциональный ряд ![]() на
промежутке IÌR. Ряд
на
промежутке IÌR. Ряд ![]() сходится равномерно на I, ряд
сходится равномерно на I, ряд ![]() сходится в
некоторой точке х0ÎЕ Þ
ряд
сходится в
некоторой точке х0ÎЕ Þ
ряд ![]() сходится равномернона " ограниченном промежутке JÌI к его сумме S(x), S(x) дифференцируема на I и
сходится равномернона " ограниченном промежутке JÌI к его сумме S(x), S(x) дифференцируема на I и ![]() .
.
Теорема 5 (об интегрируемости)
Пусть fk(x) равномерно
сходится к f(x) на [a,b] и все fk(x) интегрируемы на [a,b] по Риману (Мак-Шейну,
Курцвейлю-Хенстоку) Þ f(x) интегрируема на [a,b] в том
же смысле и ![]() .
.
Доказательство
Перейдем к интегральным суммам ![]() равномерно сходится к
равномерно сходится к
![]() на
на ![]() (так
как
(так
как ![]()
![]() ).
).
Теорема 6
Пусть функциональный ряд ![]() сходится
равномерно на [a,b] к S(x), все uk(x)
интегрируемы (в одном из 3 смыслов) на [a,b] Þ S(x) интегрируема на [a,b]
(в том же смысле) и
сходится
равномерно на [a,b] к S(x), все uk(x)
интегрируемы (в одном из 3 смыслов) на [a,b] Þ S(x) интегрируема на [a,b]
(в том же смысле) и ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.