Лекция 24
Определение 2
Свертка определенных на R функций u(x) и v(x) – это 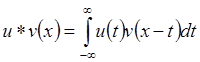 определенная в тех точках х,
где интеграл существует.
определенная в тех точках х,
где интеграл существует.
Свертка Т-периодических определенных на R
(или на (0,T)) функций u(x) и v(x) – это 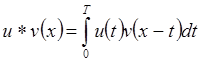 определенная
в тех точках х, где интеграл существует.
определенная
в тех точках х, где интеграл существует.
Теорема 1
Пусть u и v определенные на R и интегрируемые по Риману на " отрезке из R Þ свертка u*v $ в " точках xÎR, при выполнении одного из условий:
1) |u|2 и |v|2 интегрируемы (в несобственном смысле) на R.
2) одна из функций абсолютно интегрируема на R, а другая ограничена.
3) одна из функций финитна, то есть равна 0 вне некоторого отрезка.
Доказательство
1*) u(t)v(x-t) абсолютно интегрируема на R, так как ![]()
![]() .
.
2*) ![]() .
.
Свойства свертки
1) (Симметричность) В " точке х u*v(x) и v*u(x) одновременно существуют или несуществуют, а если $, то и равны.
Доказательство
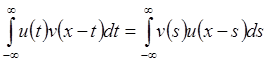 . Докажем следующую
лемму:
. Докажем следующую
лемму:
Лемма 1
Если f Т-периодическая интегрируемая на некотором отрезке Т функция Þ f интегрируема на " отрезке с длиной Т и все интегралы от f по таким отрезкам одинаковы.
Доказательство
Пусть 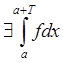 . Докажем, что
. Докажем, что 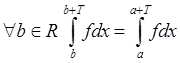 . Найдем nÎZ:
. Найдем nÎZ: ![]() . Из-за Т-периодичности:
. Из-за Т-периодичности: 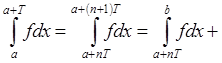
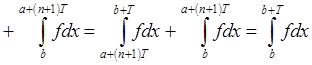 .
.
Для 1*) имеем: 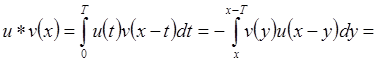
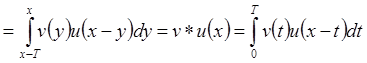 (так как функция
Т-периодическая).
(так как функция
Т-периодическая).
2) (Инвариантность относительно сдвига) Пусть ![]()
![]() .
.
Доказательство
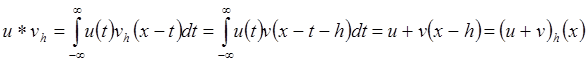 .
.
3) (О дифференцируемости) Дифференцирование свертки происходит по правилам собственных и несобственных интегралов с параметром.
Определение 2
Аппроксимативная единица (или d-образ последовательности) – это последовательность функций Kn(x) на R (на [0,T]) со свойствами:
1) 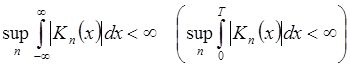 .
.
2) 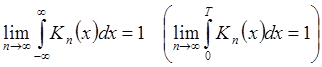 .
.
3) 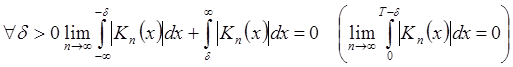 .
.
Теорема 1 (об аппроксимативной единице)
Пусть Kn(x) – аппроксимативная единица (интегрируемая по Риману) Þ если функция f определена на R (на [0,T]) и непрерывна почти всюду, то:
1) В " точке
х непрерывности f: ![]() .
.
2) Если f равномерно непрерывна
на R ( на [0,T])Þ ![]() равномерно
стремится к f(x) на R.
равномерно
стремится к f(x) на R.
3) Если Kn(x) непрерывна, а f m раз дифференцируема на R и все ее производные до m
порядка включительно ограничены и непрерывны (равномерно непрерывны на R) Þ ![]()
![]() .
.
Доказательство
1*) Рассмотрим 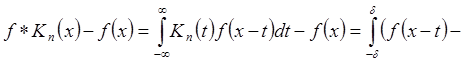
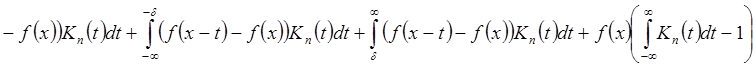
![]() для
для
![]()
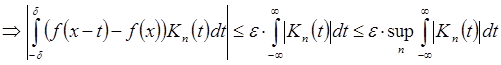 ;
;
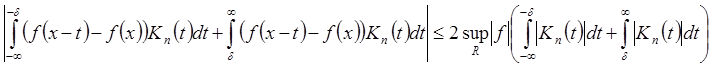 –
равномерно стремится к 0 при n®¥
по Х;
–
равномерно стремится к 0 при n®¥
по Х; 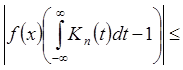
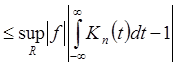 –
равномерно стремится к 0 при n®¥
по Х.
–
равномерно стремится к 0 при n®¥
по Х.
2*) Два последних члена равномерно
стремятся к 0. Для первого члена: для "
точки х: ![]() , то есть
, то есть ![]() Þ
что и требовалось доказать.
Þ
что и требовалось доказать.
В периодическом случае: 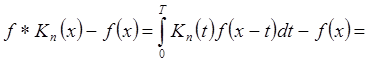
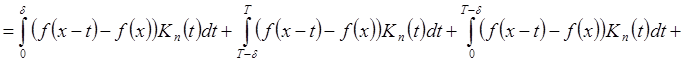
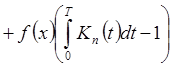 .
. ![]() для
для
![]()
![]()
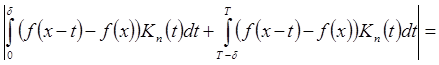
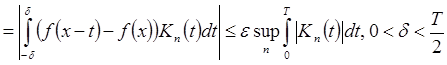 ;
;
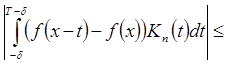
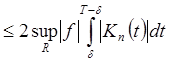 –
равномерно стремится к 0 при n®¥
по Х;
–
равномерно стремится к 0 при n®¥
по Х; 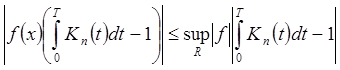 – равномерно стремится к 0
при n®¥ по Х. Аналогично для равномерной
непрерывности.
– равномерно стремится к 0
при n®¥ по Х. Аналогично для равномерной
непрерывности.
3*) 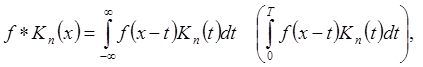
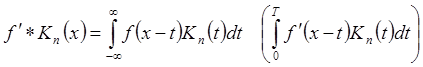 – сходятся
равномерно по признаку Вейерштрасса, так как
– сходятся
равномерно по признаку Вейерштрасса, так как ![]()
![]() и так далее. В итоге имеем:
и так далее. В итоге имеем: ![]() .
.
Пример 1 (аппроксимативной единицы)
1) 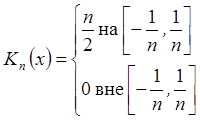 – аппроксимативная
единица на R. Продолжение Т-периодически на R – аппроксимативная единица в Т-периодическом случае.
– аппроксимативная
единица на R. Продолжение Т-периодически на R – аппроксимативная единица в Т-периодическом случае.
2) 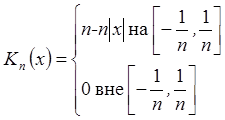 –
аппроксимативная единица на R. Продолжение с
–
аппроксимативная единица на R. Продолжение с ![]() Т-периодически
на R – аппроксимативная единица в Т-периодическом
случае.
Т-периодически
на R – аппроксимативная единица в Т-периодическом
случае.
3) Если j(x)
абсолютно интегрируема на R и 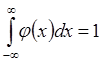 , а
, а ![]() Þ
Þ ![]() –
аппроксимативная единица.
–
аппроксимативная единица.
4) 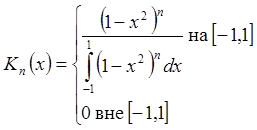 – аппроксимативная
единица на R.
– аппроксимативная
единица на R.
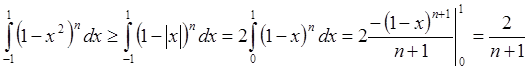 .
.
Пусть 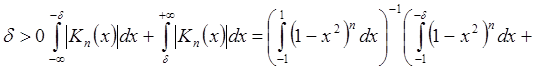
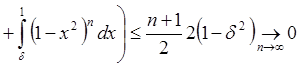 .
.
5) 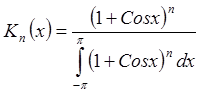 на R
– аппроксимативная единица в 2p-периодическом
случае.
на R
– аппроксимативная единица в 2p-периодическом
случае.
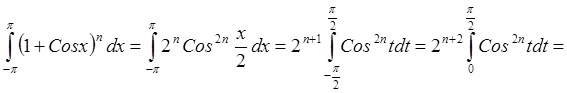
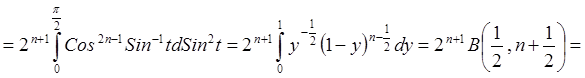
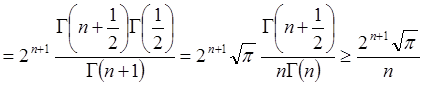 .
.
Пусть 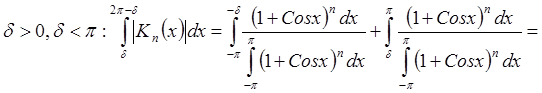
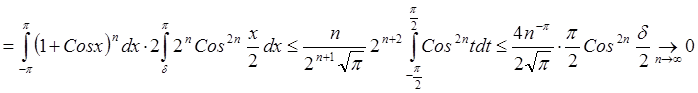
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.