Свойства измеримых функций (Доказательство и лемма 1)

Лекция 28

Определение 1

Функция f измерима на [a,b], если f определена почти всюду на [a,b] и

1) , или 2)  f(x) непрерывна на [a,b]\Е.

Свойства измеримых функций

1) Если f и j  измеримы на [a,b] Þ f±j, f×j измеримы на [a,b], а если j(х)¹0 почти всюду на [a,b], то и .

Доказательство

Возьмем e>0.  f непрерывна на [a,b]\Е и  непрерывна на [a,b]\Е Þ f±j, f×j непрерывны на . Также  непрерывна на .

2) Если f измерима на [a,b], а j  непрерывна на f([a,b]) Þ j(f) измерима на [a,b].

Доказательство

 f непрерывна на [a,b]\Е Þ j(f) непрерывна на [a,b]\Е.

3) Если f и g измеримы на [a,b] Þ  и  измеримы на [a,b].

Доказательство

4) (Обобщение свойства 3) Если f₁,…,f_n измеримы на [a,b] Þ  и  измеримы на [a,b].

Лемма 1

Пусть f_n, nÎN, измерима на [a,b],  почти всюду на [a,b] и почти всюду на [a,b] существует конечный  Þ f измерима на [a,b] и  равномерно стремится к f на [a,b]\Е при n®¥.

Доказательство

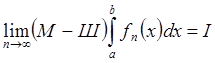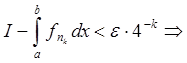
Пусть  почти всюду на [a,b] для "n Þ f_n интегрируема по Мак-Шейну и $ . Возьмем e>0 и найдем строго возрастающую последовательность натуральных n_k:  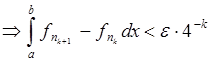. Пусть  Þ по неравенству Чебышева .  непрерывна на . Пусть  . На [a,b]\Е  равномерно стремится к f(x) при k®¥, а так как  непрерывна на [a,b]\Е Þ f непрерывна на [a,b]\Е.

. Но на [a,b]\Е:    равномерно стремится к f на [a,b]\Е при n®¥.

Рассмотрим общий случай:  почти всюду на [a,b] Þ   измерима на [a,b] и  равномерно стремится к  на [a,b]\Е при n®¥. , f(x) непрерывна на [a,b]\Е’. $ система интервалов {l_i} покрывающих  и .

Пусть  – открытое множество,  – замкнутое ограниченное множество, то есть компакт. Имеем:  равномерно стремится к  при n®¥ Þ .  .

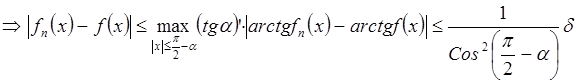Имеем, что f_n(x) равномерно стремится к f(x) на F, [a,b]\F=G,  Þ ч.т.д.

5) Если f_n, nÎN, измеримы на [a,b] и  конечен почти всюду на (a,b] Þ это измеримые функции на [a,b]. (Так как ).

6) Если f_n, nÎN, измеримы на [a,b] и  конечен почти всюду на [a,b] Þ  измеримы на [a,b]. (Так как ).

7) Если f_n, nÎN, измеримы на [a,b] и почти всюду на [a,b] $  конечный  Þ f(x) измерима на [a,b].