Лекция 32
Определение 1
![]() .
.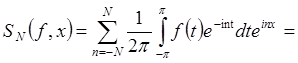
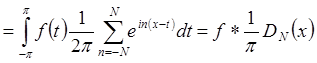 , где
, где ![]() – ядро Дирихле.
– ядро Дирихле. 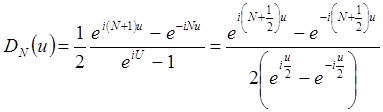
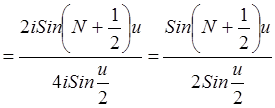 –
ядро Дирихле.
–
ядро Дирихле.
Теорема 1 (признак Дини)
Если 2p-периодическая
f интегрируемая по Мак-Шейну и в точке х для
некоторого 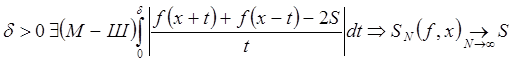 .
.
Доказательство
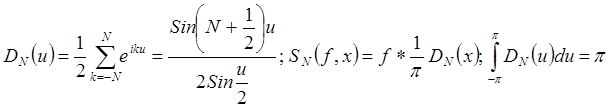 .
. 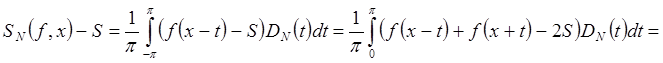
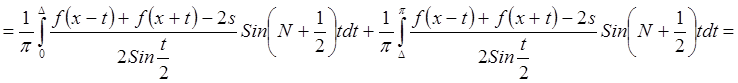
![]()
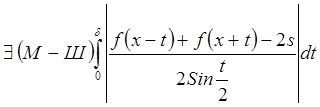
![]()
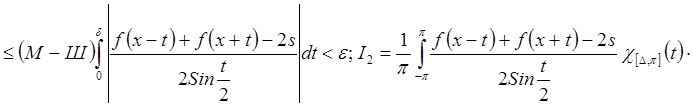
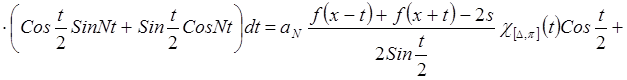
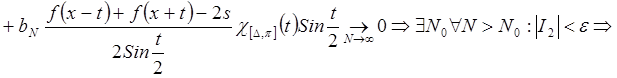 при
при
![]() .
.
Следствие 1
Если f 2p-периодическая,
интегрируема по Мак-Шейну и дифференцирована в точке х Þ ![]() (так как
(так как ![]()
![]() .
.
Следствие 2 (Принцип локализации Римана)
Если f и g 2p-периодические, интегрируемые по Мак-Шейну функции и в некоторой d-окрестности точки х f(t)=g(t) Þ ряд Фурье s[f](x) и s[g](x) одновременно сходятся или расходятся, и если сходятся, то к одному выражению.
Доказательство
![]() Þ
сходится по признаку Дини в точке х к 0.
Þ
сходится по признаку Дини в точке х к 0.
Теорема 2 (Признак Дирихле-Жордана)
Если f 2p-периодическая
функция ограниченной вариации (на [-p,p],
то есть на периоде) Þ в " точке х ![]() ,
а если f ещё и непрерывна Þ
,
а если f ещё и непрерывна Þ ![]() равномерно
стремится к f(x) на R
при N®¥.
равномерно
стремится к f(x) на R
при N®¥.
Доказательство
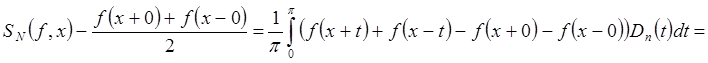
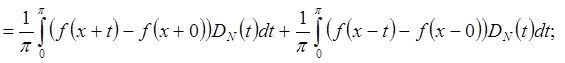
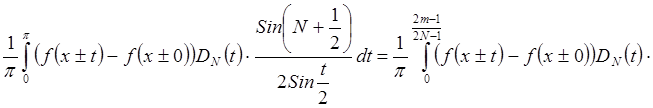
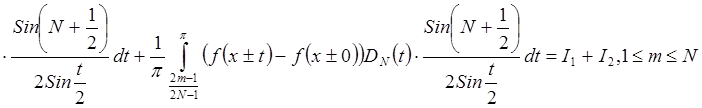
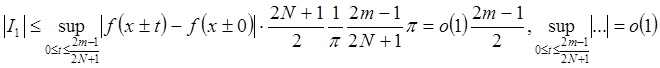 при
" фиксированном m,
то есть
при
" фиксированном m,
то есть ![]() при " фиксированном m.
при " фиксированном m. 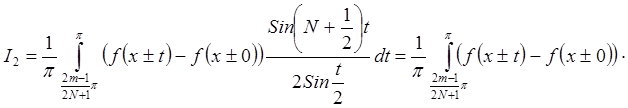
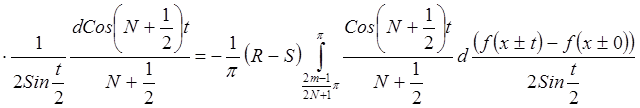 Þ
Þ
имеем 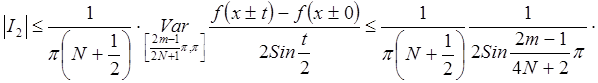
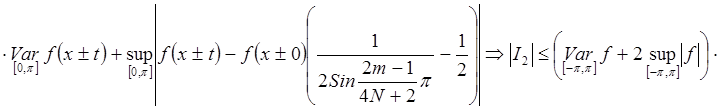
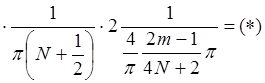 ,
так как
,
так как ![]() и
и ![]() Þ
Þ ![]() Þ имеем сходимость. Оценка 2-ого интеграла
зависит только от константы.
Þ имеем сходимость. Оценка 2-ого интеграла
зависит только от константы.
Метод суммирования (Чезаро-Фейера)
![]() .
.
Ядро Фейера 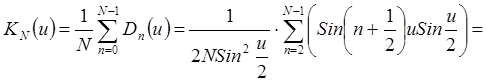
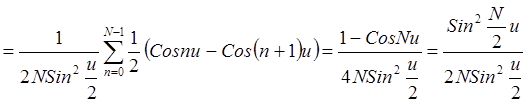 .
.
Ядро Фейера 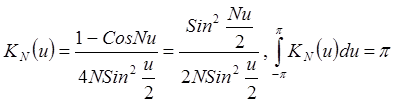 – среднее
арифметическое ядер Дирихле. Это ядро образует аппроксимативную единицу –
– среднее
арифметическое ядер Дирихле. Это ядро образует аппроксимативную единицу – ![]() . Свойства 1), 2) – очевидны.
Докажем свойство 3):
. Свойства 1), 2) – очевидны.
Докажем свойство 3): 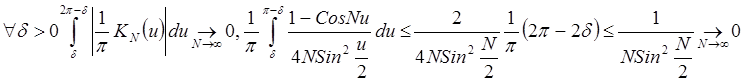
Теорема 3
Если 2p-периодическая f интегрируема
по Риману Þ в " точке непрерывности f средние-арифметические ряда Фурье ![]() , а если f непрерывна на R Þ
, а если f непрерывна на R Þ ![]() равномерно стремятся к f(x) при N®¥.
равномерно стремятся к f(x) при N®¥.
Теорема 4
Если 2p-периодическая f интегрируема
по Риману Þ в " точке непрерывности f средние Абеля (Абеля-Пуассона) ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.