Лекция 26
1) l2 (или l2) – пространство последовательностей
действительных или комплексных чисел с покоординатным сложением и умножением на
действительные или, соответственно, комплексные числа. Сумма квадратов модулей
членов последовательностей сходится, то есть ![]() .
.
Имеем, что ![]() .
.
![]() Þ
если
Þ
если ![]() то
то ![]() .
.
Так как ![]() Þ ряд
Þ ряд ![]() сходится
абсолютно, если
сходится
абсолютно, если ![]() .
. ![]()
![]()
![]() , где
, где ![]() .
.
Теорема 1
l2 – гильбертово пространство.
Доказательство
Пусть ![]() – последовательность
Коши элементов из l2, то есть
– последовательность
Коши элементов из l2, то есть 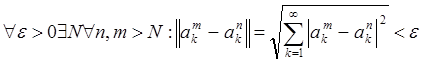 . При фиксированном k имеем неравенство:
. При фиксированном k имеем неравенство: ![]() – последовательность Коши Þ
– последовательность Коши Þ
![]() . Покажем, что
. Покажем, что ![]() – предел последовательности
– предел последовательности ![]() при n®¥ по метрике
пространства l2 и
при n®¥ по метрике
пространства l2 и ![]()
![]() .
.
Фиксируем n>N и устремим K к ¥. Имеем: ![]()
![]() .
.
Причем 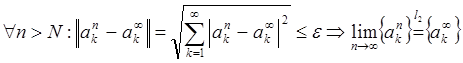 Þ ч.т.д.
Þ ч.т.д.
2) Пространство непрерывных на [a,b] (действительно- или
комплекснозначных), где 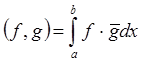 и
и 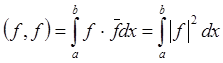 .
.
3) Пространство интегрируемых по Риману функций на [a,b]
(действительно- или комплекснозначных), где 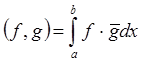 ,
причем
,
причем ![]() ,
если
,
если ![]() почти всюду на
[a,b].
почти всюду на
[a,b].
Теорема 2
Пространства в 2) и 3) – неполные пространства.
Доказательство
Рассмотрим функцию 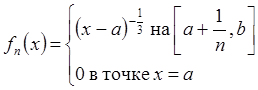 линейна на
линейна на
![]()
Если 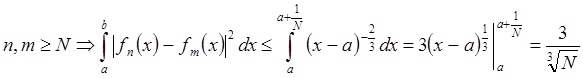 Þ
Þ ![]() на
на ![]() при
при ![]() все
все ![]() .
.
Если бы существовала ![]() (предельная
функция (по норме)) Þ
(предельная
функция (по норме)) Þ 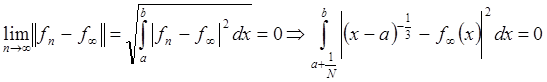 (так как нет зависимости при
(так как нет зависимости при ![]() ) Þ
) Þ ![]() почти всюду на
почти всюду на ![]() , то есть почти всюду на [a,b] Þ что и требовалось доказать.
, то есть почти всюду на [a,b] Þ что и требовалось доказать.
4) Пространство интегрируемых по Мак-Шейну
(Курцвейлю-Хенстоку) функций, квадрат модуля которых также интегрируем в том же
смысле (комплексном или действительном) на [a,b], где 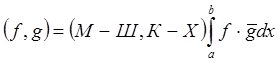 при этом
при этом ![]() , если
, если ![]() почти всюду на [a,b].
Обозначается
почти всюду на [a,b].
Обозначается ![]() .
.
Лемма 1
Пусть fn(x) –
последовательность интегрируемых по Мак-Шейну (по Курцвейлю-Хенстоку) функций
на [a,b], ![]()
![]() и
и
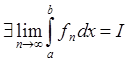 Þ f(x) интегрируемая по Мак-Шейну
(по Курцвейлю-Хенстоку) функция на [a,b] и
Þ f(x) интегрируемая по Мак-Шейну
(по Курцвейлю-Хенстоку) функция на [a,b] и 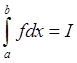 .
.
Доказательство
Возьмем 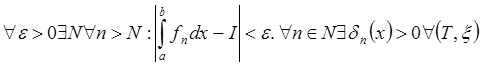 с (xÎ)
с (xÎ) 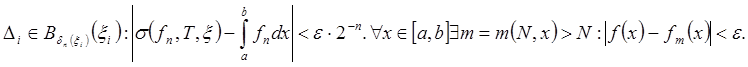
Положим ![]() на
[a,b]. Пусть (T,x) – разбиение с (xÎ)
на
[a,b]. Пусть (T,x) – разбиение с (xÎ) ![]()
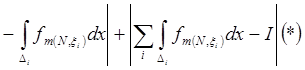 . Имеем, что
. Имеем, что ![]()
![]() ;
; 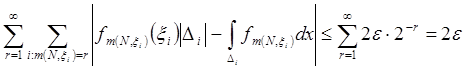 . А также,
. А также, 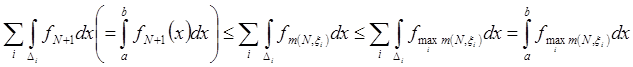 .
.
Заметим, что 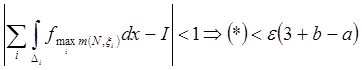 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.