Лекция 18
Теорема 1 (признак Абеля)
Если несобственный интеграл Римана 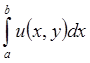 (с
особой точкой
(с
особой точкой ![]() ) сходится равномерно
на Y, функция v(x,y) определена
на
) сходится равномерно
на Y, функция v(x,y) определена
на ![]() : v(a,y)
и
: v(a,y)
и ![]() ограничена на Y Þ
несобственный интеграл Римана
ограничена на Y Þ
несобственный интеграл Римана 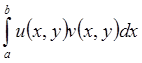 сходится
равномерно на Y.
сходится
равномерно на Y.
Теорема 2 (признак Дирихле)
Если интеграл Римана 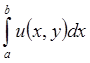 равномерно
ограничен для
равномерно
ограничен для ![]() и yÎY, а v(x,y) определена на
и yÎY, а v(x,y) определена на ![]() : v(x,y)
сходится равномерно к 0 при
: v(x,y)
сходится равномерно к 0 при ![]() и
и ![]() равномерно сходится к 0 при
равномерно сходится к 0 при ![]() Þ при условии интегрируемости по Риману u(x,y)v(x,y)
на [a,b’] при
Þ при условии интегрируемости по Риману u(x,y)v(x,y)
на [a,b’] при ![]() и
yÎY несобственный интеграл Римана
и
yÎY несобственный интеграл Римана 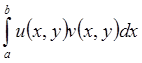 сходится
равномерно на Y.
сходится
равномерно на Y.
Доказательство
Пусть ![]() . Оценим
. Оценим 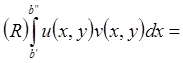
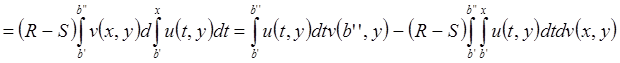 .
.
Для Теоремы 1: 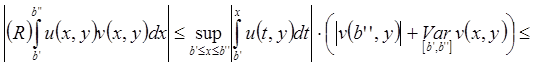
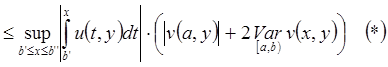 .
.
Интеграл Римана сходится равномерно Þ ![]()
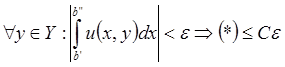 .
.
Для Теоремы 2: 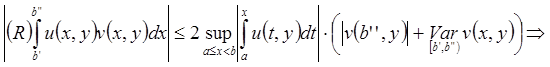
![]() и
и ![]() для
для
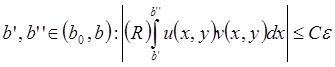 .
.
Теорема 3 (о предельном переходе)
Пусть несобственный интеграл 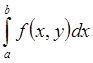 (в
" из 3 смыслов) сходится
равномерно на Y, для "bÎ[a,b) f(x,y)
равномерно стремится к g(x) на
(в
" из 3 смыслов) сходится
равномерно на Y, для "bÎ[a,b) f(x,y)
равномерно стремится к g(x) на ![]() при
при ![]() , y0
– предельная точка Y (Y из некоторого метрического пространства) Þ несобственный интеграл
, y0
– предельная точка Y (Y из некоторого метрического пространства) Þ несобственный интеграл 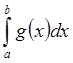 (с особой точкой b) существует и равен
(с особой точкой b) существует и равен 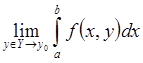 .
.
Доказательство
Имеем, что 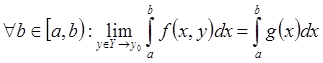 . Из-за
равномерной сходимости несобственного интеграла имеем
. Из-за
равномерной сходимости несобственного интеграла имеем 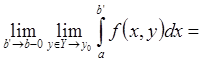
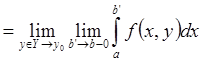 .
Имеем, что
.
Имеем, что 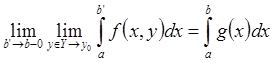 и
и 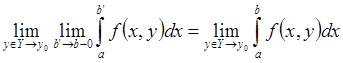 .
.
Теорема 4 (о непрерывности)
Пусть f(x,y) непрерывна на ![]() , Y –
компакт в Rn, несобственный интеграл
, Y –
компакт в Rn, несобственный интеграл 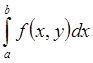 сходится равномерно на Y Þ несобственный интеграл
сходится равномерно на Y Þ несобственный интеграл 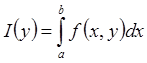 –
непрерывная функция на Y.
–
непрерывная функция на Y.
Доказательство
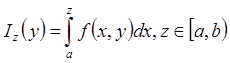 – непрерывная
функция на Y. По условию Iz(y)
равномерно стремится к I(y) на Y
при
– непрерывная
функция на Y. По условию Iz(y)
равномерно стремится к I(y) на Y
при ![]() Þ
I(y) – непрерывная функция на Y.
Þ
I(y) – непрерывная функция на Y.
Теорема 5 (о дифференцировании)
Пусть f(x,y) и ![]() непрерывные функции на
непрерывные функции на ![]() , I – промежуток
в R, несобственный интеграл
, I – промежуток
в R, несобственный интеграл 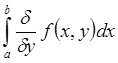 сходится равномерно на I, несобственный интеграл
сходится равномерно на I, несобственный интеграл 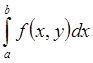 сходится
хотя бы в 1 точке I Þ несобственный интеграл
сходится
хотя бы в 1 точке I Þ несобственный интеграл 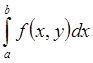 сходится равномерно на " ограниченном промежутке JÌI, это дифференцируемая функция на I
и
сходится равномерно на " ограниченном промежутке JÌI, это дифференцируемая функция на I
и 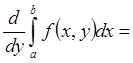
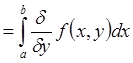 .
.
Доказательство
Рассмотрим 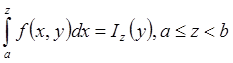 . По свойству
интеграла:
. По свойству
интеграла: 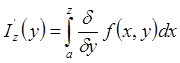 на I.
Имеем, что
на I.
Имеем, что ![]() сходится равномерно при
сходится равномерно при ![]() на Y,
то есть
на Y,
то есть ![]() равномерно стремится к
равномерно стремится к 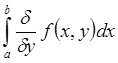 при
при ![]() на Y. Iz(y)
сходится при
на Y. Iz(y)
сходится при ![]() в некоторой точке из Y Þ
Iz(y) сходится равномерно при
в некоторой точке из Y Þ
Iz(y) сходится равномерно при ![]() на " ограниченном промежутке JÌI, то
есть Iz(y) равномерно стремится к
на " ограниченном промежутке JÌI, то
есть Iz(y) равномерно стремится к 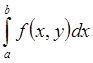 при
при ![]() на Y, причем
на Y, причем
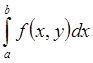 дифференцируемая на I функция и её производная – это
дифференцируемая на I функция и её производная – это 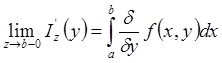 .
.
Теорема 6 (о собственном интеграле)
Пусть f(x,y) непрерывна на ![]() , и несобственный интеграл
, и несобственный интеграл 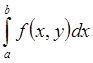 (с особой точкой b) сходится равномерно на [c,d] Þ
несобственный интеграл
(с особой точкой b) сходится равномерно на [c,d] Þ
несобственный интеграл 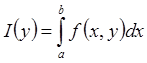 интегрируем
по Риману на [c,d] и
интегрируем
по Риману на [c,d] и 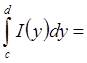
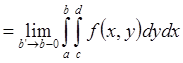 – несобственный интеграл от
– несобственный интеграл от 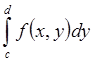 по [a,b).
по [a,b).
Доказательство
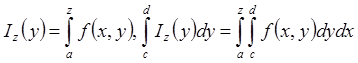 , Iz(y)
равномерно стремится к I(y) при
, Iz(y)
равномерно стремится к I(y) при ![]() на [c,d] Þ
на [c,d] Þ 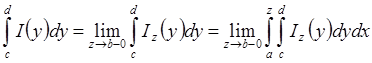 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.